Hallo Paco,
Berechne zunächst den Mittelpunkt \(M\) der Grundfläche. Dazu muss man aber wissen, welche der Punkte sich gegenüberliegen. Gegen sonstige Konventionen liegen sich hier \(A\) und \(D\) sowie \(B\) und \(C\) gegenüber. Das sieht man am besten auf einer Skizze:
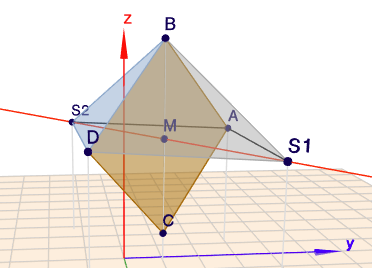
$$M = \frac 12 (A+D) = \frac 12(B+C) = \begin{pmatrix}1\\ 4\\ 13\end{pmatrix}$$Dann berechne mit dem Kreuzprodukt den Vektor \(n\), der senkrecht auf der Grundfläche steht$$n' = (B-A) \times (C-A) = \begin{pmatrix}160\\ 120\\ 0\end{pmatrix}$$Da wir nur die Richtung benötigen, skaliere ich ihn noch $$n = \frac{n'}{ \text{ggt}(160,120)} = \begin{pmatrix}4\\ 3\\ 0\end{pmatrix}$$Vom Punkt \(M\) aus liegen nun die Spitzen \(S_1\) und \(S_2\) in Richtung \(n \) 15 Längeneinheiten (LE) entfernt. Folglich ist $$S_1 = M + 15 \cdot \frac{n}{|n|} = \begin{pmatrix}13\\ 13\\ 13\end{pmatrix} \\ S_2 = M - 15 \cdot \frac{n}{|n|} =\begin{pmatrix}-11\\ -5\\ 13\end{pmatrix}$$wenn Du oben auf das Bild klickst, kannst Du die Szene im Geoknecht3D mit der Maus drehen, und bekommst so einen besseren Eindruck.
Wenn Du noch Fragen hast, so melde Dich bitte.