Die Abbildung zeigt die Dachfläche E, die ja durch die Gleichung x = (1/0/1) + s × (2/-1/1) + t × (3/1/2) beschrieben wird.
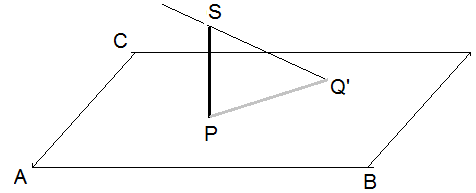
A) Um zu zeigen, dass P in der Ebene liegt, muss das System
(1) 2=1+2s+3t
(2) 2= -s+t
(3) -2=1+s+2t
eindeutig lösbar sein. Das ist es für t=1 und s= - 1.
Die Koordinaten der Spitze S des Mastes kann man bestimmen, da der Mast in x3-Richtung verläuft: S(2|2|0).
B) PQ' sei der Schatten. Dann muss zunächst Q' als Schnittpunkt von E mit \( \begin{pmatrix} x_1\\x_2\\x_3 \end{pmatrix} \)=\( \begin{pmatrix} 2\\2\\0 \end{pmatrix} \)+k·\( \begin{pmatrix} 1\\3\\-3 \end{pmatrix} \) bestimmt werden. Die Länge |\( \vec{PQ} \)| ist dann die Länge des Schattens.