Aufgabe:
Bei einer Insektenart werden im Monatsrhythmus die Stadien "Ei", "Larve" und "Insekt" durchlaufen, genauer wird die Entwicklung durch das folgende Übergangsdiagramm beschrieben:
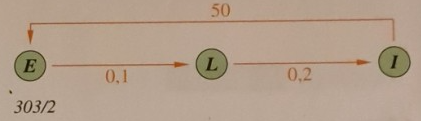
a) Geben Sie die zugehörige Übergangsmatrix \( M \) an.
b) \( M \) ist offensichtlich keine stochastische Matrix. Erläutern Sie diese Tatsache im Sachzusammenhang.
c) Ein Laborversuch startet mit 10000 Eiern. Berechnen Sie die Verteilungen für die ersten drei Monate, benutzen Sie für den zweiten und dritten Monat die Matrizenpotenzen \( M^{2} \) und \( M^{3} \).
Problem/Ansatz:
ich komme mit c) nicht weiter.