Hallo Diana,
die Gerade \(g\) durch \(A\), die senkrecht auf \(E\) steht, ist $$g: \quad \vec x = A + t \cdot \vec n$$wobei \(\vec n\) der Normalenvektor von \(E\) ist, also:$$g: \quad \vec x = \begin{pmatrix}5\\ -5\\ 1\end{pmatrix} + t \begin{pmatrix}4\\ -1\\ -1\end{pmatrix}$$Um den Schnittpunkt \(F\) von \(g\) mit \(E\) zu berechnen, setze \(g\) in die Ebenengleichung von \(E\) ein:$$E: \quad \begin{pmatrix}4\\ -1\\ -1\end{pmatrix} \vec x = 5 \\ \begin{pmatrix}4\\ -1\\ -1\end{pmatrix} \left( \begin{pmatrix}5\\ -5\\ 1\end{pmatrix} + t_F \begin{pmatrix}4\\ -1\\ -1\end{pmatrix} \right) = 5 \\ \implies t_f = -\frac{19}{18}$$Einsetzen in \(g\) liefert den Punkt \(F\) $$F = g(t_F) = \frac 1{18} \begin{pmatrix}14\\ -71\\ 37\end{pmatrix}$$ Im Bild sieht das so aus:
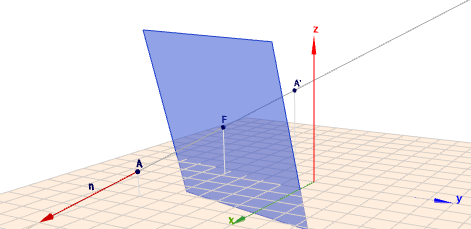
(klicke auf das Bild, dann kannst Du die Szene mit der Maus rotieren)
Für die Berechnung des Spiegelpunktes \(A'\) braucht man das \(t_F\) lediglich zu verdoppeln (überlege mal wieso!):$$A' = g(2t_F) = \frac 1{18} \begin{pmatrix}-62\\ -52\\ 56\end{pmatrix} \approx \begin{pmatrix}-3,444\\ -2,889\\ 3,111\end{pmatrix}$$Gruß Werner