Wie lauten die Koordinaten des Spiegelpunktes A?

Question

Aufgabe: Spiegelung eines Punktes

Gegeben ist E: [ Vektor X- (Vektor 2/2/1)]× (Vektor 4/-1/-1)=0 sowie der Punkt A(5/-5/1).

A Bestimmen sie eine zu E orthogonale Gerade , die den Punkt A enthält

B Bestimmen sie den Schnittpunkt F der Geraden g mit der Ebene E

C A wird an der Ebene E gespiegelt. Wie lautet die Koordinaten des Spiegempunktes A?

Answer 1

a) Der Normalenvektor ist mit $\begin{pmatrix} 4\\-1\\-1 \end{pmatrix}$ gegeben.

Die zu E orthogonale Gerade, die den Punkt A enthält, hat die Gleichung:

$\begin{pmatrix} x\\y\\z \end{pmatrix}$ =$\begin{pmatrix} 5\\-5\\1 \end{pmatrix}$ +k·$\begin{pmatrix} 4\\-1\\-1 \end{pmatrix}$.    

Comments

Und was müsste ich bei B und c machen

---

b) Geradengleichung in Ebenengleichung einsetzen uns umformen.

c) $\vec{AF}$=$\vec{FA'}$

Answer 2

Hallo Diana,

die Gerade $g$ durch $A$, die senkrecht auf $E$ steht, ist $$g: \quad \vec x = A + t \cdot \vec n$$wobei $\vec n$ der Normalenvektor von $E$ ist, also:$$g: \quad \vec x = \begin{pmatrix}5\\ -5\\ 1\end{pmatrix} + t \begin{pmatrix}4\\ -1\\ -1\end{pmatrix}$$Um den Schnittpunkt $F$ von $g$ mit $E$ zu berechnen, setze $g$ in die Ebenengleichung von $E$ ein:$$E: \quad \begin{pmatrix}4\\ -1\\ -1\end{pmatrix} \vec x = 5 \\ \begin{pmatrix}4\\ -1\\ -1\end{pmatrix} \left( \begin{pmatrix}5\\ -5\\ 1\end{pmatrix} + t_F \begin{pmatrix}4\\ -1\\ -1\end{pmatrix} \right) = 5 \\ \implies t_f = -\frac{19}{18}$$Einsetzen in $g$ liefert den Punkt $F$ $$F = g(t_F) = \frac 1{18} \begin{pmatrix}14\\ -71\\ 37\end{pmatrix}$$ Im Bild sieht das so aus:

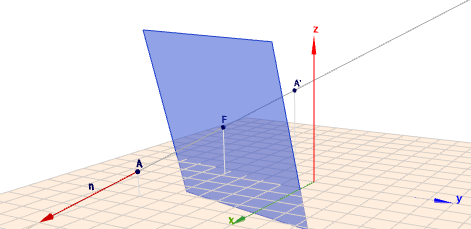
(klicke auf das Bild, dann kannst Du die Szene mit der Maus rotieren)

Für die Berechnung des Spiegelpunktes $A'$ braucht man das $t_F$ lediglich zu verdoppeln (überlege mal wieso!):$$A' = g(2t_F) = \frac 1{18} \begin{pmatrix}-62\\ -52\\ 56\end{pmatrix} \approx \begin{pmatrix}-3,444\\ -2,889\\ 3,111\end{pmatrix}$$Gruß Werner