Stelle die Hypotenuse als Funktion der kürzeren Kathete dar! Rechtwinkeliges Dreieck!

Question

 

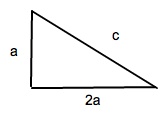
a.)  Stellen Sie eine Funktion c(a) auf, die die Länge der Hypotenuse als Funktion der Länge der kürzeren Kathete darstellt.

Meine Idee1:  a^2+a^2= c^2

Meine Idee2. HY= GK/sin α

b.) Skizieren Sie den Funktionsgrafen a ∈ ⟨ 0 ; 5 ⟩

 

Meine Idee:  ??? bitte um ausführliche Erklärung!

Comments

Meine Idee:

a^2*2a^2=c

Answer 1

Beachte: b ist hier 2a.

c^2 = a^2 + (2a)^2 = a^2 + 4a^2 = 5 a^2

c^2 = 5a^2   |√

c(a) = √5*a     Aus geometrischen Gründen kein neg. Fall.

Dabei handelt es sich um eine lineare Funktion.
Hier zwei Punkte

c(0) = 0                → P(0|0)
c(5) = √5*5 = 11.18 (ca.)       → Q(5|11.18)

P und Q in dein Koordinatensystem eintragen und dann mit dem Lineal verbinden.

Comments

WIe kommt man auf Q ????

---

Das habe ich dir ja hier:

c(5) = √5*5 = 11.18 (ca.)

vorgerechnet.

c(a) = √5*a  ordnet jedem a ein c zu. Du musst daher a in x-Richtung und c in y-Richtung eintragen. Resp. die Achsen mit a und c beschriften.

---

Bitte erkläre mir wie zu dieser Berechnung  √5*5 = 11.18  kommt!

---

Betrachte mal das Video hier: https://www.matheretter.de/wiki/koordinatensystem

Da wird erklärt, wie man Funktionsgleichungen benutzen kann um Funktionswerte auszurechnen.

c(a) = √5*a

heisst dort

y(x) = √5*x.

---

Wie kommt man zu dieser Gleichung c(a) = √5*a ????

Die Wurzel verwirrt mich etwas..