In der nachfolgenden Zeichnung sind die Funktionen f und g mit den Gleichungen

Question

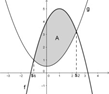
Aufgabe: In der nachfolgenden Zeichnung sind die Funktionen f und g mit den Gleichungen f(x) = –x2 + 2x + 4 und g(x) = 0,5x2 + 0,5 abgebildet. Berechnen Sie den Inhalt der von den Graphen von f und g einge-schlossenen, grau gefärbten Fläche.

1 Aufgabe:Bestimmen Sie die Schnittstellen s1 und s2      der Funktionen f und g rechnerisch entstehende Gleichungen kann man mit polyRoots lösen)
  kontrollieren Sie graphisch.
2 Aufgabe: Ermitteln Sie den Inhalt A der grau gefärb-     ten Fläche rechnerisch mit Hilfe der Integrale           ∫ss12f(x)dx und ∫ss12g(x)dx
s2
0der gleich mit ∫s1 f(x) − g(x)dx

Problem/Ansatz: Habe jetzt Längere zeit gefehlt kann, mir das jemand vorrechnen?

Text erkannt:

\( P \)

Answer 1

1. –x^2 + 2x + 4 = 0,5x^2 + 0,5  gibt x=-1 oder x=7/3

2. ∫von -1 bis 7/3  f(x) − g(x)dx = 250/27 ≈ 9,26

Comments

aber ist nicht

f(x)=g(x) also gleichsetzen

x^2+2x+4=0,5x^2+0,5

7=x^2 dannn wurzel ziehen

x1=2,6 x2=-2,6

anschließend integral b-a

=0,624

---

-x^2+2x+4=0,5x^2+0,5   | -0,5x^2 - 0,5

<=> -1,5x^2 + 2x + 3,5 = 0    | -1,5

 <=>    x^2  -4/3 x -7/3 = 0

mit pq-Formel x = 2/3 ±√ (4/9 + 21/9 )

                      = 2/3 ±√25/9 =  2/3 ± 5/3

                      x=7/3 oder x=-3/3= -1