eine kleine Skizze - muss nicht maßstabsgetreu sein - ist bei solchen Aufgaben immer hilfreich:
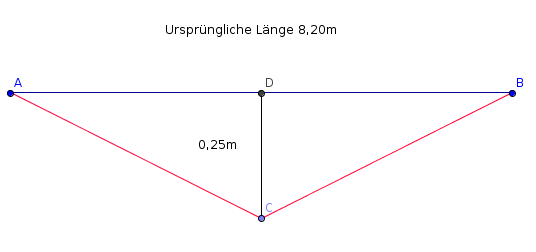
Die ursprüngliche Länge des Seils war 8,20m (blaue Strecke).
Die neue Länge des Seils ist die Summe der beiden roten Strecken.
Da wir jeweils ein rechtwinkliges Dreieck vorliegen haben, beträgt eine rote Strecke nach dem Satz des Pythagoras:
√[(8,20/2)2 + 0,252]
und die Gesamtlänge des gestreckten Seils damit
2 * √(4,102 + 0,252)
Um wieviel wurde das Seil also gestreckt?
2 * √(4,102 + 0,252) - 8,20 ≈ 0,01523
Das Seil wurde um ca. 0,01523 m gestreckt, also um ca. 1,523 cm.
Besten Gruß