y' = 2·x·y^2
Lass uns doch mal einsetzen
(- 1/(x^2 + c))' = 2·x·(- 1/(x^2 + c))^2
2·x/(x^2 + c)^2 = 2·x/(x^2 + c)^2
Und die Lösung von Wolfram
(1/(x^2 - c))' = 2·x·(1/(x^2 - c))^2
- 2·x/(x^2 - c)^2 = 2·x/(x^2 - c)^2
Demnach wäre die Lösung von Wolfram falsch. Ich prüfe mal Wolfram selber
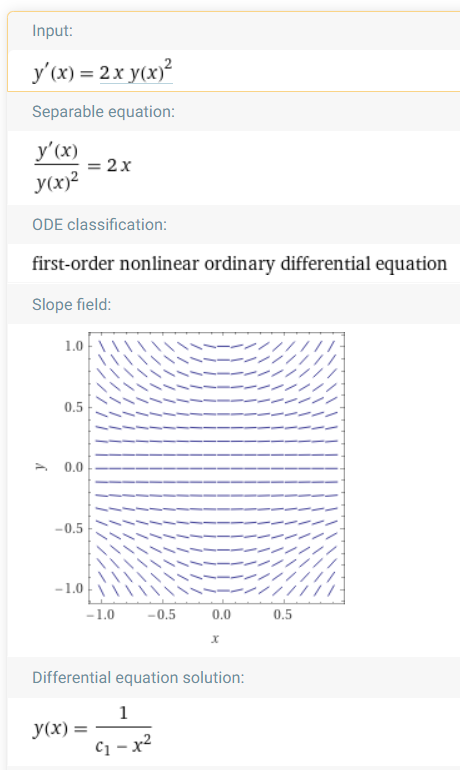
Wolfram nennt hier
y = 1/(c - x^2) und nicht wie von dir genannt y = 1/(x^2 - c)
Wo liegt da der Hund begraben?