Hallo,
das macht man mit dem Skalarprodukt. Ist \(\varphi\) der Winkel zwischen zwei (Spalten-)Vektoren \(\vec u\) und \(\vec v\), dann gilt$$\cos \varphi = \frac{\vec u^T \cdot \vec v}{|\vec u|\cdot |\vec v|}$$Konkret in diesem Fall$$\begin{aligned}\cos \varphi &= \frac{\begin{pmatrix}2 \\ -1 \\ 2\end{pmatrix}^T \cdot \begin{pmatrix}4 \\ 0 \\ -3\end{pmatrix}}{\left|\begin{pmatrix}2 \\ -1 \\ 2\end{pmatrix}\right| \cdot \left|\begin{pmatrix}4 \\ 0 \\ -3\end{pmatrix}\right|} \\&= \frac{2\cdot 4 + (-1)\cdot 0 + 2\cdot (-3)}{\sqrt{2^2 + (-1)^2+2^2}\, \cdot \sqrt{4^2 + (-3)^2}} \\&= \frac{2}{3 \cdot 5} = \frac 2{15} \\ \implies \varphi &\approx 82,3° \end{aligned}$$
Ich habe das mal im Geoknecht3D eingegeben. Der berechnete Winkel scheint zu stimmen ...
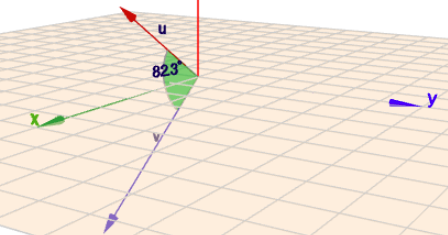
(klick auf das Bild)