Rekonstruktion: Sattelpunkt des Graphen ist Ws(1/0)

Question

Aufgabe:

Der Sattelpunkt des Graphen einer ganzrationalen Funktion 4. Grades ist Ws(1/0), der Hochpunkt H(-2/4,5).

Problem/Ansatz:

Kann jemand bei der Rechnung behilflich sein?

Answer 1

Du kennst f(1), f'(1), f''(1), f(-2) und f'(-2).

5 Gleichungen genügen für 5 Unbekannte.

Comments

Das heißt? wie bzw. was rechnet man dann aus

---

Was weißt du über den Wert vom Ableitungen

- an einer Extremstelle

- an einer Sattelstelle?

---

Allgemein oder auf die Aufgabe bezogen?

---

Wenn du es allgemein weißt, kannst du es auf die konkrete Aufgabe anwenden.

Answer 2

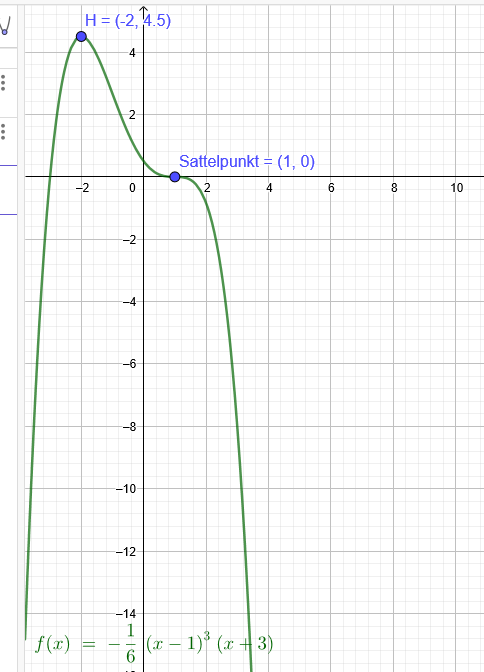
Hier der Weg über die Nullstellenform der Parabel 4.Grades:

Der Sattelpunkt des Graphen einer ganzrationalen Funktion 4. Grades ist Ws(1|0), der Hochpunkt H(-2|4,5).

f(x)=a*(x-1)^3*(x-N)

H(-2|4,5):

f(2)=a*(-2-1)^3*(-2-N)=-27a*(-2-N)=27a*(2+N)

1.)27a*(2+N)=4,5  → a=\( \frac{4,5}{54+27N} \)

f(x)=\( \frac{4,5}{54+27N} \)*[(x-1)^3*(x-N)]

f´(x)=\( \frac{4,5}{54+27N} \)*[3*(x-1)^2*(x-N)+(x-1)^3]

f´(-2)=\( \frac{4,5}{54+27N} \)*[3*(-2-1)^2*(-2-N)+(-2-1)^3]

\( \frac{4,5}{54+27N} \)[27*(-2-N)-27]=0

-2-N-1=0

N=-3

a=\( \frac{4,5}{54+27*(-3)} \)=\( \frac{4,5}{54-81} \)= - \( \frac{1}{6} \)

f(x)= - \( \frac{1}{6} \)*(x-1)^3*(x+3)

Comments

Vielen lieben Dank wirklich!