Hessenormalform Vektoren Winkel und Abstände

Question

Aufgabe

Gegeben sind das Parallelogram Abcd mit A (2/1/3),B(0/5/1),C(-3/5/4),D(-1/1/6) sowie ein innerer Punkt vom Rechteck N(-1,5/4/3,5) und die Spitze S(4/8/9)der Pyramide
Die Pyramide wird vom Punkt N aus senkrecht zur Grundfläche durchbohrt. Untersuchen Sie, ob dabei das Dreieck Abs oder das Dreieck Bcs durchstoßen wird.

Comments

Du hast ja schon die richtigen Stichworte.

wahrscheinlich auch ne Zeichnung? sonst kannst du die mit Geozeichner 3d erstellen.

wo liegen jetzt deine Schwierigkeiten?

lul

---

Was genau muss ich jetzt tun? Ich verstehe es nicht.

---

hallo die Senkrechte  auf die Fläche die du durch die Hesseform kennst  durch N  legen und mit der Fläche schneiden, dann feststellen in welchen Dreieck der Schnitt Punkt liegt

lul

---

Ich kann die Grundfläche doch auch ganz normal bestimmen ohne hesseform oder nicht? Und dann einfach den n vektor der Grundfläche durch Punkt N laufen lassen daraus ne Koordinatengleichung machen und dann den Schnittpunkt mit einer der beiden Dreiecke bestimmen oder nicht?

Answer 1

Hallo René,

.. sonst kannst du die mit Geozeichner 3d erstellen.

wie soll das ein Fragesteller schaffen, wenn es die Leute, die hier antworten nicht machen (können?). Ich habe im folgenen Bild auch nur eingetragen, was in der Aufgabenstellung steht:

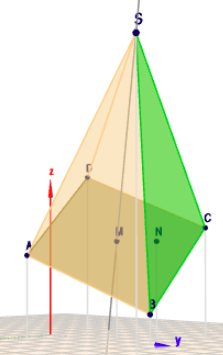
Ich kann die Grundfläche doch auch ganz normal bestimmen ohne hesseform oder nicht?

Für die Gerade, die senkrecht zur Grundfläche verläuft, benötigst Du den Normalenvektor der Grundfläche. Berechne diesen aus dem Kreuzprodukt$$\vec{AB} \times \vec{AD} = \begin{pmatrix}12\\ 12\\ 12\end{pmatrix} = 12 \begin{pmatrix}1\\ 1\\ 1\end{pmatrix}$$

Und dann einfach den n vektor der Grundfläche durch Punkt N laufen lassen

Wenn Du mit 'n vektor' den Normalenvektor meinst, dann ist das genau der obige.

und dann den Schnittpunkt mit einer der beiden Dreiecke bestimmen

Ja genau - wähle die Ebene durch die Punkte \(BCS\).

Weißt Du wie man feststellt, ob sich ein Punkt der Ebene innerhalb dieses Dreiecks befindet?

Comments

Warum muss ich eine Ebene durch die Punkte BCS erstellen? Nur zum errechnen des Schnittpunktes? Ich soll doch mit der geraden mit dem Ortsvektor N und dem richtungsvektor (dem N vektor der Grundfläche) den Schnittpunkt mit einem der Dreiecke bestimmen? Oder verstehe ich die Aufgabe falsch?

Ja einfach Ebenen gleichsetzen und dann über ein LGS die schnittgerade bestimmen oder bei einer Gerade ebene selbe schema nur Schnittpunkt berechnen

---

Warum muss ich eine Ebene durch die Punkte BCS erstellen? Nur zum errechnen des Schnittpunktes?

Ja genau dafür.

Ich soll doch mit der geraden mit dem Ortsvektor N und dem richtungsvektor (dem N vektor der Grundfläche) den Schnittpunkt mit einem der Dreiecke bestimmen?

Das ist korrekt. Wie willst Du den den "Schnittpunkt mit einem der Dreiecke" bestimmen, ohne die Ebene zu kennen, in der das Dreieck liegt?

Ja einfach Ebenen gleichsetzen und dann über ein LGS die schnittgerade bestimmen ...

nach "Schnittgeraden" ist hier nicht gefragt. Welche Ebenen meinst Du denn dann?

Tipp: klicke auf das Bild in meiner Antwort.

---

Nur zum errechnen des Schnittpunktes?

Na ja - streng genommen musst Du den Schnittpunkt gar nicht errechnen. Es reicht aus, die Parameter aus der Parameterform der Ebene durch \(BCS\) zu berechnen.

---

Ich meine natürlich Gerade Ebene Schnittpunkt bestimmen. Nicht Ebene Ebene.

Noch eine Frage. Wieso muss ich den Schnittpunkt mit dem anderen Dreieck nicht bestimmen? Ich muss doch auch zeigen, dass das andere Dreieck nicht geschnitten wird oder etwa nicht bzw. es wird ja irgendwann geschnitten, aber nicht in der Pyramide. (Die Ebene läuft ja weiter) und das muss ich doch zeigen, dass der Schnittpunkt nicht in der Pyramide liegt oder?

---

Wieso muss ich den Schnittpunkt mit dem anderen Dreieck nicht bestimmen?

Die Gerade durch \(N\) schneidet die Dreiecksfläche \(BCS\) in \((1|\,6,5|\,6)\). Wenn das der Fall ist, dann muss das Dreieck \(ABS\) nicht mehr überprüft werden. So wie die Gerade verläuft, kann sie nur eines der vier Seitendreiecke der Pyramide schneiden.

---

Ja stimmt. Macht Sinn. Vielen Dank!!
!!