Wie berechne ich folgenden Abitur Aufgaben?

Question

In dieser Aufgabe werden unterschiedliche mathematische Modelle für den Verlauf eines derartigen Bogens betrachtet(Gateway Arch aus St. Louis). Dabei entspricht die x-Achse dem Erdboden und die y-Achse zeigt vertikal nach oben. Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Wirklichkeit.

1.) Das erste Modell beschreibt den Verlauf eines Bogens, der die Höhe s hat. Die Breit des Bogens am Erdboden soll wie beim Gateway Arch mit seiner Höhe übereinstimmen. Der linke Fußpunkt des Bogens liegt im Koordinatenursprung und der rechte Fußpunkt auf der positiven x-Achse.

a.) Ermittle eine Funktionsgleichung einer in R definierten quadratischen Funktion in Abhängigkeit von s, die den Verlauf dieses Bogens beschreibt.

Für s ∈ R, s>0 ist die Funktion f_s mit

f_s (x) = -4/sx² + 4x, mit x element R,

definiert. Verwende in b) und c) dieses Modell für den Verlauf des Bogens.

b) Bei einer Errichtung des Bogens wird auf 75 % der endgültigen Höhe s des Bogens eine Plattform parallel zum Erdboden eingezogen, die von der einen Seite des Bogens bis zu anderen reicht.

Berechne die Breite dieser Plattform in Abhängigkeit von s.

c) Berechne den inneren Winkel zwischen Bogen und Erdboden am linken Fußpunkt des Bogens.

Im Folgenden wird die Höhe des Bogens auf 100 Meter festgelegt. Der Boden wird modellhaft durch die in R definierte Funktion f₁₀₀ mit

f₁₀₀(x) = -0.04x² + 4x

und ihren Graphen G_f100 dargestellt.

d) Berechne für dieses Modell die Fußpunkte und gib den höchsten Punkt des Bogens an.

Berechne unter angabe einer Stammfunktion die Größe der Fläche zwischen dem Bogen und dem Erdboden.

Comments

Okay. Jetzt mach dir mal die Mühe und reiche die Aufgabe als PDF-Dokument nach. Außerdem wäre es schön, eine genaue Quellenangabe zu haben.

---

Clemens hat die Frage überarbeitet.

Answer 1

Wenn das eine Abitur Aufgabe ist dann besorge dir einfach die Lösungen zu den Aufgaben und dann sagst du vielleicht was du an den Lösungen nicht verstehst.

Zur Not könnte ich auch meine Sammlung von Abituraufgaben durchgehen. Wenn du sagst aus welchem Bundesland und Jahr, das eine Abituraufgabe war, könnte ich auch bestimmt mit einer Lösung aushelfen.

Comments

Ich hatte gerade Mathe Langzeit

Ich hab’s eigentlich gut bearbeiten können 3/4 geschafft ...

Answer 2

Hi,

a.)  Ich habe die Kernidee mal in der Graphik skizziert. Wir wissen, aus der Aufgabenstellung, dass der Bogen immer durch den Ursprung gehen soll. Wir folgern hieraus $P_0=(0,0)$. Weiter können wir der Aufgabenstellung die Punkt $P_1 = \left(\frac{s}{2}, \,s\right)P_2=(s|0)$ entnehmen, $P_1$ ist der Hochpunkt in Abhängigkeit zu $s$ und $P_2$ ist die rechte "Ecke" des Bogens.

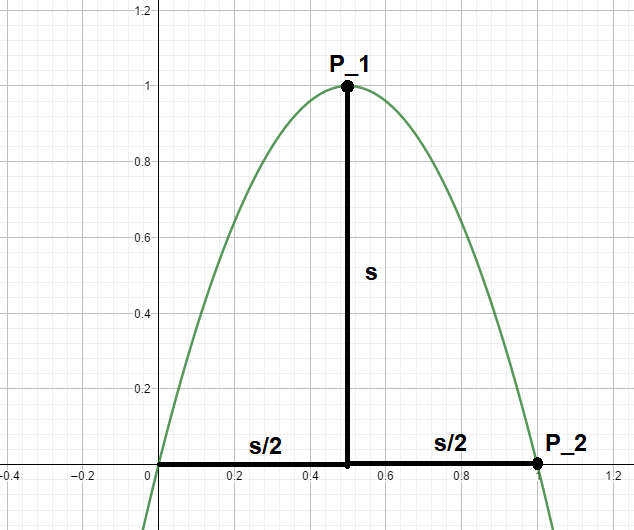
Jetzt wissen wir, dass die Normalparabel folgendermaßen definiert ist:

$$f(x) = ax^2 +bx +c$$

Ich setze nun der Reihe nach die Punkte in diese Gleichung und baue mir somit die gesuchte Funktion in Abhängigkeit zu $s$.
$$f(0) = a\cdot 0^2 +b\cdot 0 + c = 0,\quad c = 0$$
$$f(s) = a\cdot s^2 +b\cdot s = 0,\quad b = -as$$
$$f(s/2) = a\cdot (s/2)^2 +b\cdot (s/2) = s$$
Einsetzen, auflösen nach $a, \, b$ liefert dann:
$$a = -\frac{4}{s}, \quad b = 4$$
damit:
$$f_s(x) = -\frac{4}{s}x^2+ 4x$$

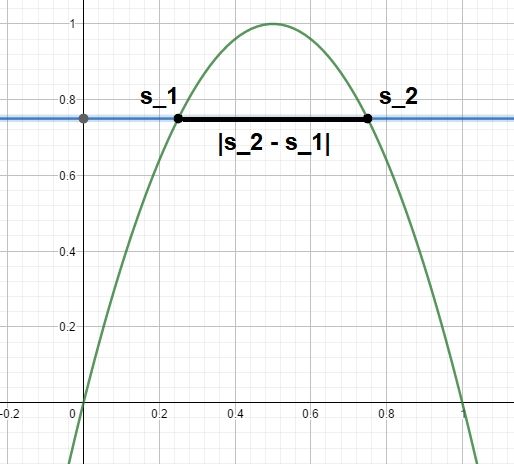
b.) In 75% der Höhe soll nun eine Plattform errichtet werden. Mit anderen Worten haben wir hier also eine Konstante Funktion mit $\frac{3}{4}s$. Die Breite der Plattform erhalten wir, indem die Gleichung der konstanten Funktion mit der der Parabel in Abhängigkeit zu $s$ gleichgesetzt wird. Wir lösen also:
$$\frac{3}{4}s = -\frac{4}{s}x^2+ 4x$$
und kommen auf folgende Lösungen:
$$s_1 = \frac{1}{4}s, \quad s_2 = \frac{3}{4}s$$
Die Breite der Plattform resultiert dann aus:
$$|s_2-s_1| = |\frac{3}{4}s - \frac{1}{4}s| = \frac{1}{2}s$$



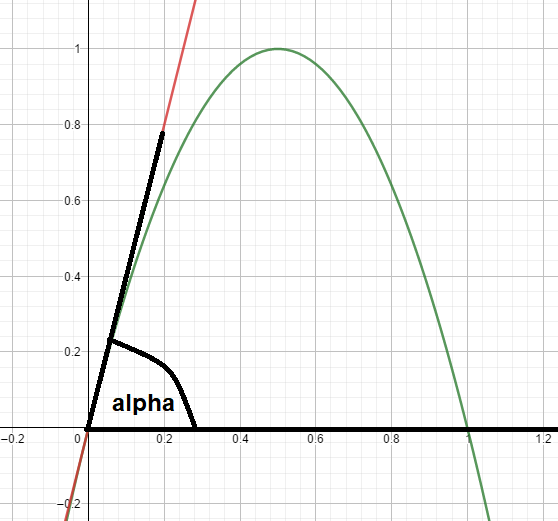
c.)  Für die Berechnung des inneren Winkels zwischen Bogen und Erdboden am linken Fußpunkt des Bogens konstruiere ich eine Tangente, die durch den Punkt $P_0=(0,0)$ geht und die entsprechende Steigung der Parabel an diesem Punkt besitzt. Die erste Ableitung von $f_s(x)$ sagt mir etwas über die Steigung. Ich berechne also zuerst die Ableitung:
$$f_s(x) = -\frac{4}{s}x^2+ 4x$$
$$f_s'(x) = -\frac{8}{s}x+ 4$$
ich setze den Punkt $P_0=(0,0)$ in $f_s'(x)$ ein, um die Steigung an dieser Stelle zu erhalten:
$$f_s'(0) = -\frac{8}{s}0+ 4$$
$$f_s'(0) = 4$$
Die Tangente geht durch den Ursprung und besitzt die Steigung $m=4$, daraus folgt:
$$t(x) = 4x$$
Als nächstes kann der Winkel zwischen der Tangente und der X-Achse über den Tangens (arctan) ermittelt werden, wir erinnern uns:
$$\tan(\alpha) = m$$
$$\alpha = \arctan(4) = 75,9637°$$

PS: Sehr sehr schade, dass die Frage nicht mehr die original Bilder enthält...