Untervektorraum - Mengen

Question

Aufgabe: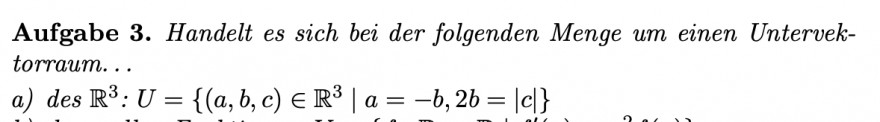

Text erkannt:

Aufgabe 3. Handelt es sich bei der folgenden Menge um einen Untervektorraum...
a) des \( \mathbb{R}^{3}: U=\left\{(a, b, c) \in \mathbb{R}^{3}|a=-b, 2 b=| c \mid\right\} \)

Das ist laut Lösung kein Untervektorraum aber ich frage mich, wie man das mathematisch mit Rechnung beweist (und nicht nur ein Gegenbeispiel findet).

Vielen Dank für die Hilfe

Answer 1

Aloha :)

Es ist \((-1|1|-2)\in U\), aber für den negativen Vektor gilt \((1|-1|2)\not\in U\), weil \(b=\frac{|c|}{2}\ge0\) sein muss. Daher ist die Abgeschlossenheit bezüglich der Skalarmultiplikation verletzt.

Was hast du gegen eine Gegenbeispiel? Das reicht doch völlig aus.

Comments

aaahhhh achso, danke für die Erklärung! :)