Aloha :)
Diese Gleichung kannst du nicht geschlossen nach \(x\) auflösen. Du kannst die Gleichung aber numerisch lösen. In solchen Situationen ist das Newton-Verfahren zur Bestimmung von Nullstellen oft eine gute Wahl.$$f(x)\coloneqq(-2,7x+242)\cdot e^{0,01x}-220\stackrel!=0$$Bei diesem Verfahren startet man mit einem Schätzwert \(x_0\) und bestimmt die Tangente in diesem Punkt:$$t(x)=f(x_0)+f'(x_0)\cdot(x-x_0)$$Dann schaut man, bei welchem \(x\)-Wert diese Tangente die \(x\)-Achse schneidet und nimmt diesen Schnittpunkt \(x_1\) als neuen Schätzwert:$$0\stackrel!=t(x_1)=f(x_0)+f'(x_0)\cdot(x_1-x_0)\quad\implies\quad x_1=x_0-\frac{f(x_0)}{f'(x_0)}$$Die Rekursionsgleichung beim Newton-Verfahren ist daher:$$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$$
Wir bestimmen noch die Ableitung$$f'(x)=-2,7\cdot e^{0,01x}+(-2,7x+242)\cdot0,01\cdot e^{0,01x}$$und setzen sie in die Rekursionsgleichung ein:
$$x_{n+1}=x_n-\frac{(-2,7x+242)e^{0,01x}-220}{-2,7\cdot e^{0,01x}+(-2,7x+242)\cdot0,01\cdot e^{0,01x}}$$$$\phantom{x_{n+1}}=x_n-\frac{-2,7x+242-220e^{-0,01x}}{-0,027x-0,28}$$$$\phantom{x_{n+1}}=x_n+\frac{242-2,7x-220e^{-0,01x}}{0,027x+0,28}$$
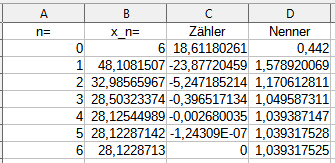
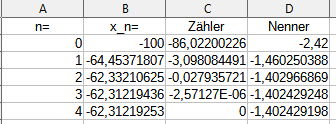
Das liefert uns als Lösungen:$$x_1=28,1228712954388\quad;\quad x_2=-62,3121925262902$$