Hilfe Vektoren herausfinden Tipp

Question

Ich benötige Hilfe bei der Aufgabe a) siehe Foto.

Thema: Analytische Geometrie (Vektoren)

Vielen Dank

Text erkannt:

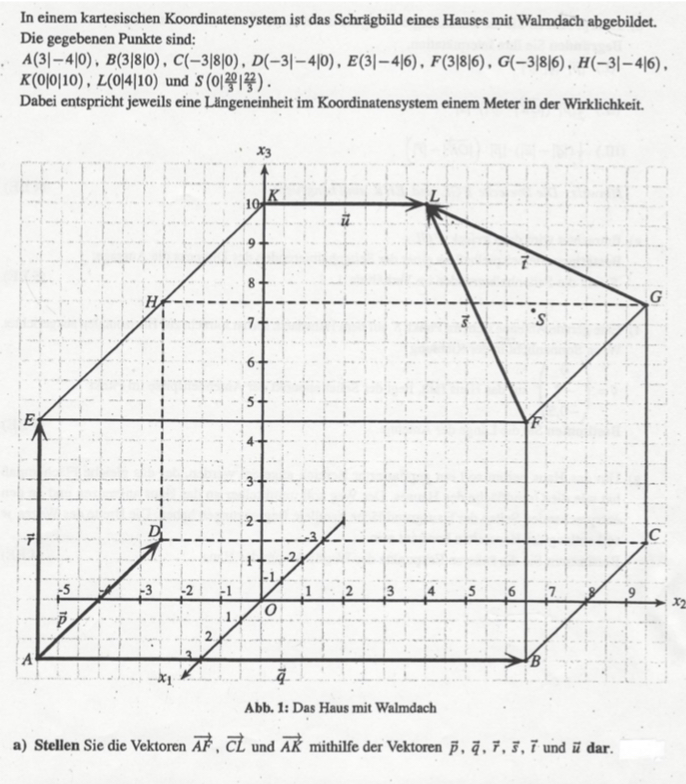
In einem kartesischen Koordinatensystem ist das Schrăgbild eines Hauses mit Walmdach abgebildet. Die gegebenen Punkte sind
\( A(3|-4| 0), B(3|8| 0), C(-3|8| 0), D(-3|-4| 0), E(3|-4| 6), F(3|8| 6), G(-3|8| 6), H(-3|-4| 6) \)
\( K(0|0| 10), L(0|4| 10) \) und \( S\left(\left.0\right|^{2}\right. \)
Dabei entspricht jeweils eine Längeneinheit im Koordinatensystem einem Meter in der Wirklichkeit
Abb. 1: Das Haus mit Walmdach
a) Stellen Sie die Vektoren \( \overrightarrow{A F} \), \( \overrightarrow{C L} \) und \( \overrightarrow{A R} \) mithilfe der Vektoren \( \vec{p}, \vec{q}, \vec{r}, \vec{s}, \vec{t} \) und \( \vec{u} \) dar.

Answer 1

Suche einfach einen Weg (z.B. beim ersten ) von A nach F

etwa den Weg ABF und versuche die "Etappen" des

Weges durch die gegebenen Vektoren zu beschreiben.

Es ist ja AB=q und BF=r (Denn BF ist

parallel gleichlang und gleichorientiert zu r) also

gilt \( \overrightarrow{A F} = \vec{q}+\vec{r}\).

etc. Das kann auch über mehrere Etappen gehen.

Oder CL ergibt den Weg CGL also

\( \overrightarrow{C L} = \vec{r}+\vec{t}\).

Comments

Achso, also muss ich nichts rechnen?

Wäre dann CL = r+t

?

---

Genau, habe ich gerade ergänzt.

---

Oh super!

Dann wäre AK= r+s

?

Sind Sie sicher dass man nichts rechnen muss?

---

Könnte ich auch für AK = q + r +s + u

gehen?

---

Rechnen muss man nicht, aber für AK wäre ja der Weg

ABFLK

(denn EK ist nicht parallel zu s ) , also ist es

q+r+s-u

---

Vielen Dank, Sie haben mir sehr geholfen! LG und bleiben Sie gesund :))

---

Hier noch mal ein Bild zur Veranschaulichung.

Ein Weg vom Punkt \(A\) zum Punkt \(K\) führt über die Vektoren \(q\), \(r\), \(s\) und \(-u\).$$\vec{AK} = q+r+s-u$$\(-u\) deshalb, weil auf diesem Weg der Vektor \(u\) in der Gegenrichtung von L nach K durchlaufen wird.

Du kannst die Vektoren beliebig verschieben solange sie ihre Richtung, Orientierung und Länge beibehalten. Hier wurde der Vektor \(r\) so verschoben, dass er die Punkte B und F verbindet.

Wenn Du auf das Bild klickst, öffnet sich Geoknecht3D und man kann die Szene mit der Maus rotieren.

Answer 2

Male einfach die verlangenten Vektoren in deine Figur.

Dann in der gleichen Farbe einen Streckenzug, der diesen Vektor als Summe hat.

Dann dort diejenigen Vektoren in Kleinbuchstaben anschreiben, die gegeben sind, anschreiben (immer noch in der gleichen Frabe.

Nun meist nur noch ablesen

Auf + und - achten

Bsp. AF = AB + BF = q + r

Ergänze Pfeile über meinen Vektoren.

usw.

Comments

Tut mir leid, aber ich habe dass nicht verstanden. Könnten Die es nochmal erklären?

---

Es folgen sicher noch mehr Erklärungen. Welches Wort verstehst du nicht?

"a) Stellen Sie die Vektoren \( \overrightarrow{A F} \), \( \overrightarrow{C L} \) und \( \overrightarrow{A R} \) mithilfe der Vektoren \( \vec{p}, \vec{q}, \vec{r}, \vec{s}, \vec{t} \) und \( \vec{u} \) dar."

Das wolltest du wissen.

Weisst du denn, wie man geometrisch Vektoren addiert?

---

Ja das wieß ich

Answer 3

Jeder Punkt kann durch einen Ortsvektor angegeben werden: So wird A(3|-4|0) dargestellt durch den Ortsvekor \( \vec{OA} \)=\( \begin{pmatrix} 3\\-4\\0 \end{pmatrix} \). Dann wird z,B. \( \vec{AB} \) dargestellt als \( \vec{OB} \)-\( \vec{OA} \).

Comments

Wie soll das an der Aufgabe angewendet werden?

---

Zum Beispiel so:

\( \vec{AB} \)=\( \vec{q} \)=\( \begin{pmatrix} 3\\8\\0 \end{pmatrix} \)--\( \begin{pmatrix} 3\\-4\\0 \end{pmatrix} \)=\( \begin{pmatrix} 0\\12\\0 \end{pmatrix} \).