Ableitung, Tangente und Normale

Question

Aufgabe:

Miriana behauptet

durch jeden Punkt des Graphen von f =x³−6 gibt es zwei Geraden, die Tangenten dieses Graphen sind

Prüfe diese Behauptung ohne Rechnung ausführlich, inden du Skizzen anfertigst und präzisiere gegebenenfalls Mirians Behauptung. Begründe deine Antwort und belege deine Ergebnisse in Spezialfällen rechnerisch.
Problem/Ansatz:

Es ist ganz kompliziert und weiß nicht, was gemeint ist.

Comments

Die Behauptung:

Durch jeden Punkt des Graphen von f(x) =x³−6 gibt es zwei Geraden, die Tangenten dieses Graphen sind.

ist falsch, wenn sie Tangenten in diesem Punkt sind.

Beweis: Zwei verschiedene Geraden haben zwei verschiedene Steigungen. Dann müsste f(x) an jeder Stelle x zwei verschiedene Ableitungen haben. Die Ableitung ist aber an jeder Stelle x ohne Ausnahme f '(x)=3x². Zu jedem x gibt es genau ein f '(x).

Answer 1

Hallo

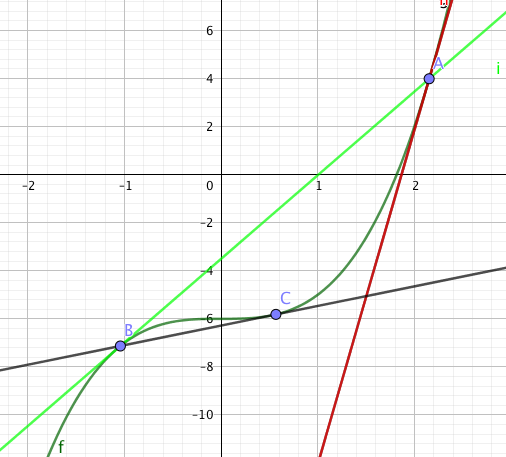
dass es in jeden Punkt eine Tangente in dem Punkt gibt ist klar, wegen der Punktsymmetrie zu (0,-6) gibt es durch den Punkt eine zweite Gerade, die dann Tangente an einem anderen Punktest. meine Skizze in A ist die rote Gerade Tangente in Am die grüne Tangente in B, in B ist die grüne Tangente  die schwarze Tangente in C,

(in der Skizze ist der Maßstab auf x und y- Achs verschieden. damit man es deutlicher sieht )

Gruß lul

Comments

Sehr schöne Illustration.

Ich verstehe den ersten Satz leider nicht ganz.

Wie genau legst du die zweite Gerade im Punkt P(0|-6)?

---

Hallo

P=(0,-6) ist der Wendepunkt und Symmetriepunkt. Ich lege von A =(x1,y1) aus eine Tangente nach B=(x2,y2) mit  der Steigung m=f'(x2) und m=(y2-y1)/(x2-x1)

oder eine beliebige Gerade durch A die nur A und einen weiteren Schnittpunkt (= Berührpunkt) mit f(x) hat.

Gruß lul

---

Ok. Danke

Berührpunkt heisst für mich "zusätzlich gleiche Steigung" wie die berührende Gerade. Das ist mE bei P(0|-6) nicht möglich. (D.h. mE ist der Wendepunkt als Ausnahmepunkt aus der Behauptung auszuschliessen. Bei den illustrierten Punkten A und B kann ich deine Argumentation gut verstehen.) https://de.wikipedia.org/wiki/Ber%C3%BChrung_(Mathematik)

---

Danke , Ja, das hatte ich übersehen der Wendepunkt hat halt eine "Doppelgerade" entsprechend einer "doppelten Nullstelle" ;-)

lul