Der Graph einer ganzrationalen Funktion f 3. Grades besitzt den Hochpunkt H (2/0), schneidet die y-Achse im Punkt (0/-4) und hat an der Stelle x=-1 einen Wendepunkt.
a. Bestimmen Sie den Funktionsterm
f(x) = ax^3 + bx^2 + cx + d
f(2) = 0
8·a + 4·b + 2·c + d = 0
f'(2) = 0
12·a + 4·b + c = 0
f(0) = -4
d = -4
f''(-1) = 0
2·b - 6·a = 0
Das LGS liefert die Lösung a = - 1/7 ∧ b = - 3/7 ∧ c = 24/7 ∧ d = -4
f(x) = -1/7x^3 - 3/7x^2 + 24/7x - 4
b.Bestimmen Sie die Extrem- und Wendepunkte
Extrempunkte f'(x) = 0
- 3·x^2/7 - 6·x/7 + 24/7 = 0
Lösung über abc-Formel bei x = -4 ∨ x = 2
f(-4) = -108/7 = -15.42857142
f(2) = 0
Damit ist der Tiefpunkt bei (-4 | -15,4) und der Hochpunkt (2 | 0).
Wendepunkt f''(x) = 0
- 6·x/7 - 6/7 = 0
x = -1
f(-1) = -54/7 = -7,7
Damit ist der Wendepunkt bei (-1 | -7,7)
c.Bestimmen Sie die Gleichung der Tangente und der Normale im Wendepunkt
f'(-1) = 27/7
t(x) = 27/7 * (x + 1) - 54/7
n(x) = -7/27 * (x + 1) - 54/7
d. Zeichnen Sie den Graphen Gf im Bereich -3 ≤ x ≤ 2

e. Gegeben ist die Parabel g(x)= x^2-4x+5. Berechnen Sie den Schnittpunkt von f und g
-1/7x^3 - 3/7x^2 + 24/7x - 4 = x^2 - 4x + 5
Über ein Näherungsverfahren finden wir eine Lösung bei x = -14.02725084.
f(-14.02725084) = 257.8727693
g(-14.02725084) = 257.8727694
Schnittpunkt ist bei (-14,0 | 257,9)
f
. Vom Punkt ( 1/-2) aus, können zwei Tangenten an den Graphen von g gelegt werden. Bestimmen Sie die Koordinaten der Berührpunkte u1 und u2 und geben sie die Tangentengleichungen an.
(g(x) - (-2)) / (x - 1) = g'(x)
(x^2 - 4·x + 7)/(x - 1) = 2·x - 4
Wir finden hier eine Lösungen bei x = 3 ∨ x = -1
g(3) = 2
g'(3) = 2
g(-1) = 10
g'(-1) = -6
Die Berührpunkte liegen bei (3 | 2) und (-1 | 10)
Die Tangentengleichungen lauten
t1(x) = 2*(x - 3) + 2
t2(x) = -6*(x + 1) + 10
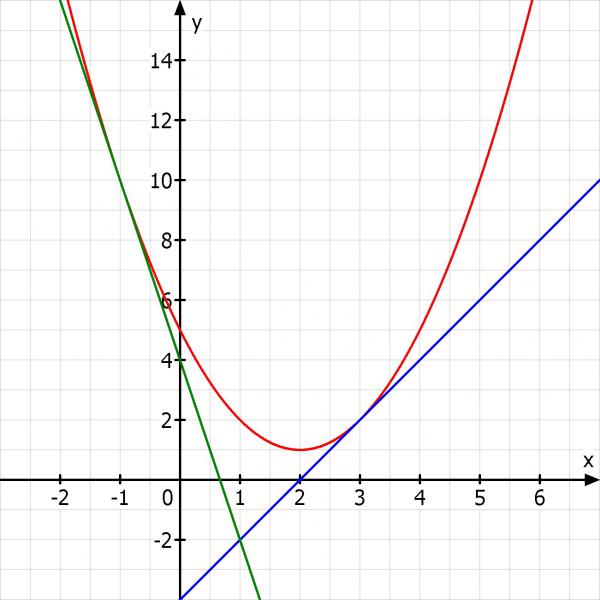
Hier noch eine Skizze: