Hallo, tut mir leid das ich die Buchseite fotografieren musste, aber der Scanner hat das nicht erkannt. Ich nehme die Frage sofort wieder raus wenn ich Antworten habe.
Ich bin wirklich am verzweifeln, kann mir bitte jemand eine Aufgabe verrechnen.. wäre prima.
Mein Lehrer erklärt mir die Aufgaben morgen, aber bis dahin möchte ich was in der Hand haben.
Text erkannt:
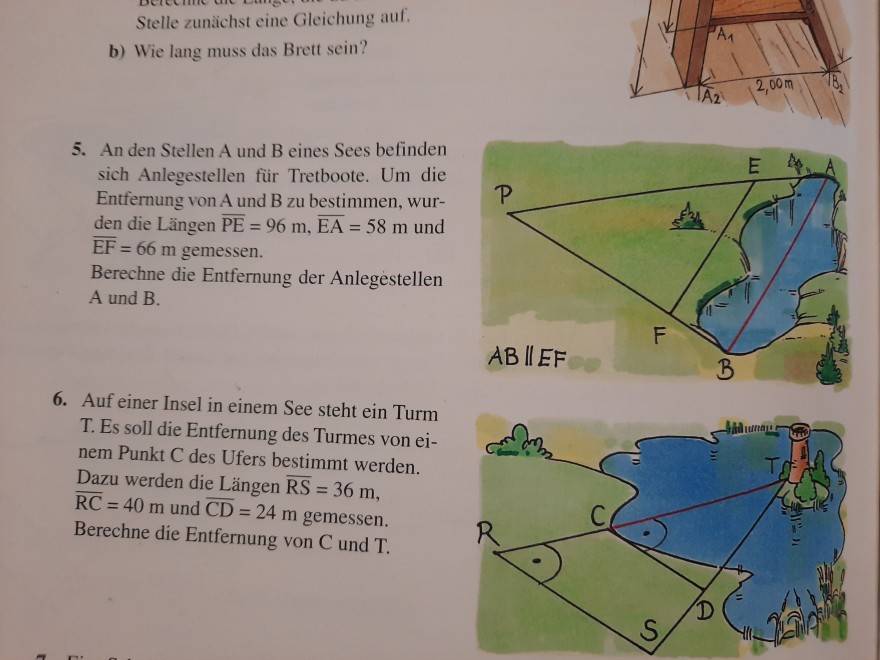
Stelle zunächst eine Gleichung auf.
b) Wie lang muss das Brett sein?
5. An den Stellen A und B eines Sees befinden sich Anlegestellen für Tretboote. Um die Entfernung von A und B zu bestimmen, wurden die Längen \( \overline{\mathrm{PE}}=96 \mathrm{~m}, \overline{\mathrm{EA}}=58 \mathrm{~m} \) und
\( \overline{\mathrm{EF}}=66 \mathrm{~m} \) gemessen.
Berechne die Entfernung der Anlegestellen A und B.
6. Auf einer Insel in einem See steht ein Turm T. Es soll die Entfernung des Turmes von ei- nem Punkt C des Ufers bestimmt werden. Dazu werden die Längen \( \overline{\mathrm{RS}}=36 \mathrm{~m} \),
\( \mathrm{RC}=40 \mathrm{~m} \) und \( \overline{\mathrm{CD}}=24 \mathrm{~m} \) gemessen
Berechne die Entfernung von \( \mathrm{C} \) und \( \mathrm{T} \).