Hallo,
Dann sieht das Trapez wohl so aus
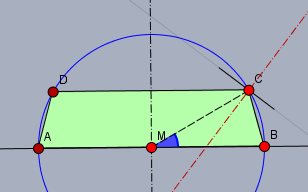
Für den den Punkt \(C\) ist der Punkt auf dem Einheitskreis zu finden, bei dem das Trapez \(ABCD\) maximalen Umfang besitzt. Geometrisch lässt sich diese Position leicht finden. Mit folgender Überlegung:
So wie auf dem ersten Bild gezeigt, nimmt der Umfang zu, wenn \(\alpha\) (blau) vergrößert wird, weil \(|CB|\) schneller wächst als \(|CD|\) kleiner wird, da man davon ausgehen kann, dass die Summe der Strecken \(|BC| + |CD|\) genau dann unverändert bleibt, wenn sich der Punkt \(C\) senkrecht zur WInkelhalbierenden von \(\angle DCB\) (rot) bewegt. Auf diesem Bild ..
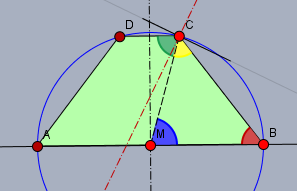
.. dagegen nimmt der Umfang bei Vergrößerung von \(\alpha\) wieder ab, da nun die Strecke \(|CD|\) schneller verkürzt wird, als \(|BC|\) bei der Bewegung von \(C\) anwächst.
Konsequenz: der Umfang ist genau dann maximal, wenn die Winkelhalbierende (rot) von \(\angle DCB\) durch den 'Drehpunkt' \(M\) verläuft. Daraus folgt:$$\angle DCM \text{ (grün) } = \angle MCB \text{ (gelb) } \implies U \to \max$$und da \(\triangle MBC\) ein gleichschenkliges Dreieck ist und damit \(\angle MCB\) (gelb) gleich \(\angle CBM\) (rot) ist und die Summe der drei Winkel \(=180°\) sein muss, ist$$\angle MCB = 60° \implies \alpha_{\max} = 60°$$
Mit dem Lagrange-Multiplikator sieht das so aus: ich setze \(x = \cos \alpha\) und \(y = \sin \alpha\). Zu maximieren ist$$U = 2 + 2(x + \sqrt{(1-x)^2 + y^2}) \to \max$$das ist die Hauptbedingung. Die Nebenbedigung ist, dass \(C\) auf dem Kreis liegt$$x^2 +y^2 - 1 = 0$$Lagrange-Gleichung aufstellen und Ableiten gibt$$\begin{aligned} L(x,y,\lambda) &= 2 + 2(x + \sqrt{(1-x)^2 + y^2}) + \lambda(x^2 +y^2 + 1) \\ \frac{\partial L}{\partial x} &= 2\left(1 + \frac{x-1}{\sqrt{(1-x)^2 + y^2}} \right) + 2\lambda x= 0 \\ \frac{\partial L}{\partial y} &= 2\left( \frac{y}{\sqrt{(1-x)^2 + y^2}}\right) + 2\lambda y= 0 \\ \end{aligned}$$Multipliziere die erste Gleichung mit \(y\), die zweite mit \(x\) und beide mit dem Wurzelterm, dann erhält man$$\begin{aligned} 2y \sqrt{(1-x)^2 + y^2} + 2y(x -1)&= 2xy &&|\, \div 2y \\ \sqrt{(1-x)^2 + y^2} + x - 1 &= x &&|\, -x+1 \\ \sqrt{(1-x)^2 + y^2} &= 1 &&|\,{}^2 \\ 1- 2x + \underbrace{x^2 + y^2}_{=1} &= 1 &&|\, -1+2x \\ 1 &= 2x \\ \implies x&= \frac 12\end{aligned}$$Mit \(x_{\max} = 1/2\) folgt dann$$x_{\max} =\frac 12 =\cos \alpha_{\max} \implies \alpha_{max} = 60°$$Gruß Werner
PS.: der Lagrange-Ansatz ist hier ein wenig übertrieben. Man kann \(x^2+y^2=1\) auch gleich in der Hauptbedingung einsetzen. An der eigentlichen Rechnung ändert sich aber dadurch nichts.