Ein ebenes Viereck ist genau dann ein Parallelogramm..

Question

Aufgabe:

Gegeben ist im R^2 oder R^3
ein ebenes Viereck mit den
Eckpunkten A, B, C und D. Ferner sei der Punkt S der
Schnittpunkt der beiden Diagonalen.
Beweisen Sie vektoriell: Ein ebenes Viereck ist genau
dann ein Parallelogramm, wenn sich die Diagonalen hal-
bieren.

Answer 1

Hallo Miriam,

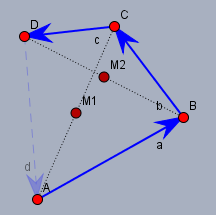
Ist ein beliebiges Viereck mit den Ecken A, B, C und D in \(\mathbb R^2\) oder \(\mathbb R^3\) gegeben, so lassen sich seine vier Seiten schreiben als$$\vec a = \vec{AB} \\ \vec b = \vec{BC} \\ \vec c = \vec{CD} \\ \vec d = \vec {DA}$$ Die Mittelpunkte der beiden Diagonalen sind ausgehend vom Punkt \(A\)$$\vec m_1 = \frac 12 (\vec a + \vec b) \\ \vec m_2 = \vec a + \frac 12 (\vec b + \vec c)$$Mit der Bedingung, dass diese sich gegenseitig halbieren gilt$$\vec m_1 = \vec m_2$$Einsetzen gibt$$\begin{aligned} \frac 12 (\vec a + \vec b) &=  \vec a + \frac 12 (\vec b + \vec c) \\ \vec a + \vec b &= 2 \vec a + \vec b + \vec c \\ \vec 0  &= \vec a + \vec c \\ \implies \vec c &= -\vec a \\ \implies \vec d &= -(\vec a + \vec b + \vec c) = -\vec b \end{aligned}$$Das bedeutet, dass die jeweils gegenüberliegenden Seiten parallel und gleich lang sind. Die letzte Zeile folgt aus \(\vec a + \vec b + \vec c + \vec d = \vec 0\).

Daraus folgt: halbieren sich die Diagonalen gegenseitig, so ist das Viereck ein Parallelogramm.