Wie ist diese Aufgabe zu rechnen? Gibt es Formeln?

Question

Aufgabe:

Problem/Ansatz: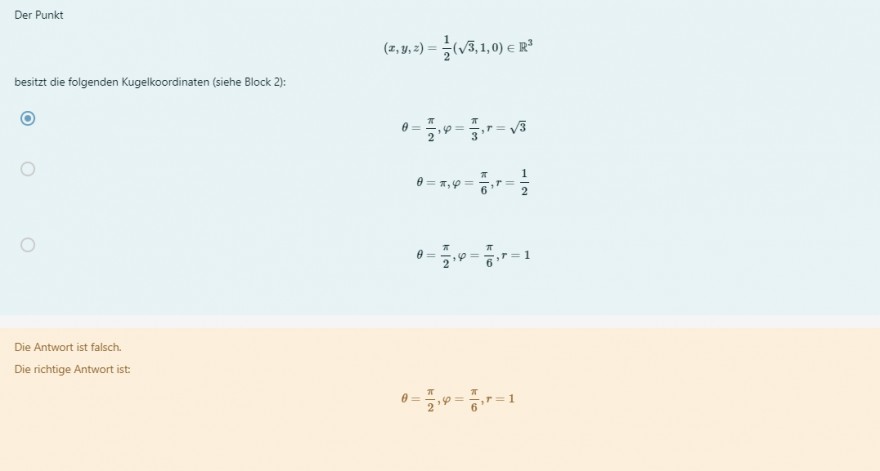

Text erkannt:

Der Punkt
$$ (x, y, z)=\frac{1}{2}(\sqrt{3}, 1,0) \in \mathbb{R}^{3} $$
besitzt die folgenden Kugelkoordinaten (siehe Block 2):
O
$$ \theta=\frac{\pi}{2}, \varphi=\frac{\pi}{3}, r=\sqrt{3} $$
0
$$ \begin{array}{l} \theta=\pi, \varphi=\frac{\pi}{6}, r=\frac{1}{2} \\ \theta=\frac{\pi}{2}, \varphi=\frac{\pi}{6}, r=1 \end{array} $$
Die Antwort ist falsch.
Die richtige Antwort ist:
$$ \theta=\frac{\pi}{2}, \varphi=\frac{\pi}{6}, r=1 $$

Wie ist diese Aufgabe zu lösen, wer kann mir helfen?

Comments

Da die Werte für r in den Antworten unterschiedlich sind, musst du hier nicht wissen, wie die Winkel berechnet werden.

Wende Pythagoras an und schon hast du die Lösung.

Answer 1

Gegenfrage: Warum hast du die erste Antwort angeklickt?

Dein Punkt hat doch vom Ursprung gar nicht den Abstand \( \sqrt{3} \).

Comments

Das war geraten meine Frage war: Wie ist diese Aufgabe zu lösen, wer kann mir helfen?
Ich weiß nur nicht wie ich diese aufgabe lösen soll bzw. was für einen ansatz etc.

---

Du musst die Antwort anklicken, bei der alle 3 Werte stimmen.

Ich konkretisiere meine Frage.

We berechnest du den Abstand r des Punktes \((x, y, z)=\frac{1}{2}(\sqrt{3}, 1,0) \) vom Ursprung?