Stellen Sie die nachstehenden Funktionen f : R → R als Verkettung f = h ◦ g dar. Hierbei seien g und h von der identischen Abbildung verschieden. Geben Sie auch jeweils möglichst große Definitionsbereiche für g und h an!
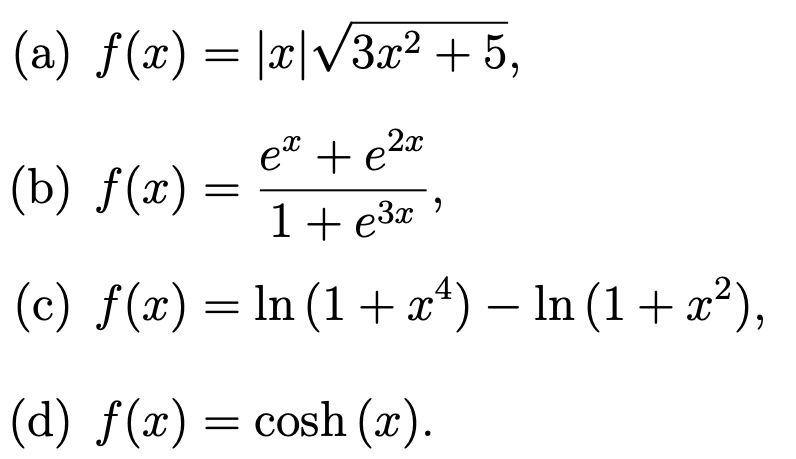
Text erkannt:
(a) \( f(x)=|x| \sqrt{3 x^{2}+5} \)
(b) \( f(x)=\frac{e^{x}+e^{2 x}}{1+e^{3 x}} \)
(c) \( f(x)=\ln \left(1+x^{4}\right)-\ln \left(1+x^{2}\right) \)
(d) \( f(x)=\cosh (x) \)
Ich bin ehrlich gesagt vollkommen überfordert. Ich habe mich jetzt bestimmt 2h quer durch meine Vorlesungsunterlagen und Google durchgelesen, um irgendwelche Regeln für eine "Endkettung" zu finden. Leider bin ich auf nichts brauchbares gestoßen. Gibt es irgendeinen Trick?
Ich verstehe das Prinzip der Verkettung. Und auch, wie man (wenn man verkettet) die Definitionsbereiche bestimmt. Aber so wie ich das verstehe, muss ich es in der Aufgabe "von hinten aufrollen." Bei einer "einfachen" Funktion z.B. (2x)^2 würde ich die Verkettung "rauslesen", aber bei den obigen Aufgaben weiß ich nicht, wo ich anfangen soll.
Für Tipps wäre ich sehr sehr dankbar.
Liebe Grüße & bleibt gesund
