Wie schreibt man das auf?

Question

Zeichne jeweils die beiden Geraden und bestimme die Schnittpunkte

a) \( G((1,2),(1,3)), G((-1,2),(-1,-1)) \)
b) \( G((3,0),(1,4)), G((-1,-3), G(2,2)) \)

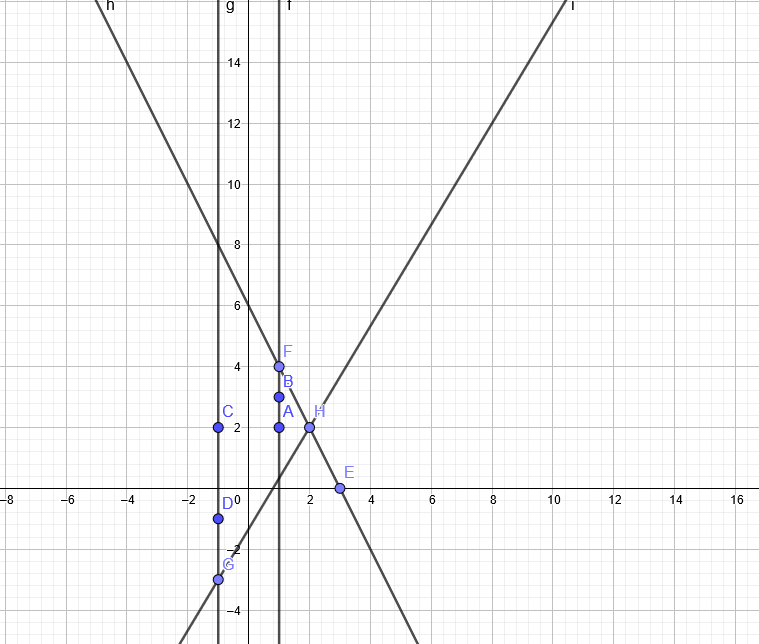Also meine frage ist, dass bei dieser Aufgabe bei a) kein schnittpunkt gibt. Wie schreibt man das auf?

Answer 1

x=-1 und x=1 gleichgesetzt, ergibt einen Widerspruch. {(x|y) mit x=1}∩{(x|y) mit x=-1}={   }.

Comments

Also danke erstmal.

Wie heißt die Schnittpunkt der Geraden mit der dieser Menge.

\( \left\{(x, y) \in \mathbb{R}^{2} \mid x^{2}+y^{2}=4\right\} \)

Also ich weiß schon, wo die schnittpunkte sind, nur weiß ich nicht wie man das aufschreibt.

---

Welche der Geraden ist gemeint?

---

Da steht, der Schnittpunkt der Geraden. Ich geh davon aus, dass alle geraden gemeint ist, bis auf das ganz rechts.

---

Na, dann:

Schnittpunkt von Kreis und h: y=5/3·x-3:

x²+(5/3·x-4/3)²=4

Ausmultiplizieren, ordnen, quadratische Gleichung lösen:

x₁=\( \frac{10+3√30}{17} \);  x₂=\( \frac{10-3√30}{17} \)

in Kreisgleichung einsetzen:

y₁=\( \frac{6+5√30}{17} \);  y₂=\( \frac{6-5√30}{17} \).

---

... nur weiß ich nicht wie man das aufschreibt.

wenn der Kreis \(K\)$$K= \left\{(x, y) \in \mathbb{R}^{2} \mid x^{2}+y^{2}=4\right\} $$ist, und z.B. die Gerade \(G_0((1,2),(1,3))\) $$G_0 = \left\{(x, y) \in \mathbb{R}^{2}\mid x=1\right\}$$dann ist die gemeinsame Schnittmenge $$K \cap G_0 = \left\{  (x, y) \in \mathbb{R}^{2} \mid y^2=3 \land x=1\right\}$$und bei \(G_2((3,0),(1,4))\)$$G_2 = \left\{ (x, y) \in \mathbb{R}^{2}\mid 2x+y = 6 \right\}$$die Schnittmenge ist leer$$K \cap G_2 = \left\{  \right\}$$und bei \(G_3((-1,-3), \,(2,2))\) könnte man ohne Rechnung schreiben$$K \cap G_3 = \left\{ (x, y) \in \mathbb{R}^{2}\mid x^{2}+y^{2}=4 \land 5x-3y=4 \right\}$$

---

Kann mir jemand beii dieser aufgabe helfen?

https://www.mathelounge.de/844911/schnitt-zweier-kreise-entweder-kreis-besteht-keinem-punkt

Ich wäre sehr dankbar