Grenzwertberechnung: lim x->0 ( (1/sin(x)) - (1/x) )
Ich frage mich bei Grenzwertaufgaben, ob man sofort mit dem Rechnen aufhören kann und die Lösung raus hat, sobald kein "0/0" oder "unendlich/unendlich" mehr raus kommt.
Siehe dieses Beispiel, ich habe "0/2" rausbekommen, wollte dann noch weiter rechnen, aber mir ist aufgefallen, dass ich dann in eine Endlosschleife geraten würde:
Text erkannt:
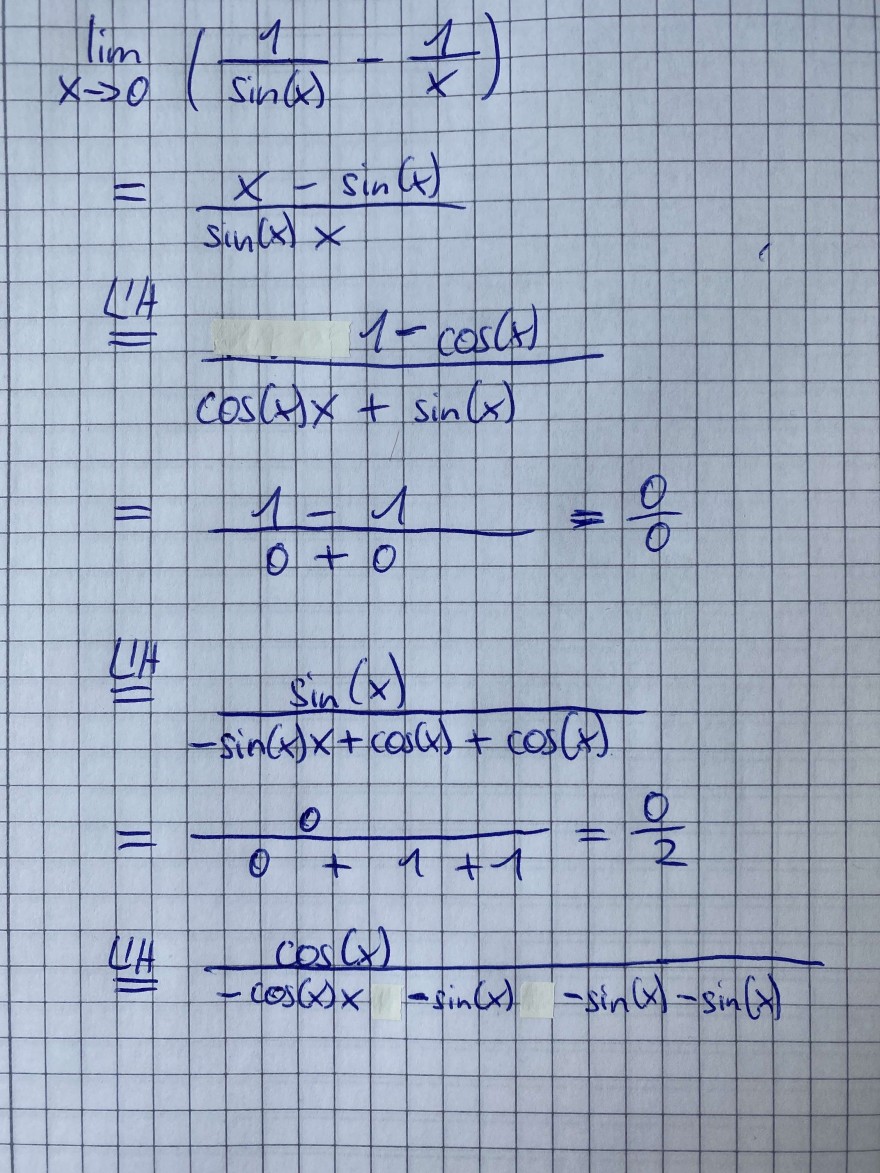
\( \lim \limits_{x \rightarrow 0}\left(\frac{1}{\sin (x)}-\frac{1}{x}\right) \)
\( =\frac{x-\sin (x)}{\sin (x) x}=\frac{0}{1-\cos (x)} \)
\( =\frac{\sin (x)}{\cos (x) x+\sin (x)}=\frac{1-1}{0+0}=\frac{0}{-\sin (x) x+\cos (x)+\cos (x)} \)
\( =\frac{0}{0+1+1}=\frac{0}{2} \)
\( \quad=\frac{\cos (x)}{=\cos (x) x-\sin (x)-\sin (x)-\sin (t)} \)
Vielen Dank für Antworten vorab!