Aufgabe:

Text erkannt:
Aufgabe 6: Bestimme Sie alle Matrizen
$$ A:=\left(\begin{array}{cc} x & y \\ z & w \end{array}\right) $$
die zur Matrix
$$ B:=\left(\begin{array}{ll} 1 & 1 \\ 0 & 1 \end{array}\right) $$
kommutativ sind. Es soll also gelten \( A \cdot B=B \cdot A \).
Problem/Ansatz:

Text erkannt:
Aufgabe 6: Bestimme Sie alle Matrizen
$$ A:=\left(\begin{array}{cc} x & y \\ z & w \end{array}\right) $$
die zur Matrix
$$ B:=\left(\begin{array}{ll} 1 & 1 \\ 0 & 1 \end{array}\right) $$
kommutativ sind. Es soll also gelten \( A \cdot B=B \cdot A \).

Text erkannt:
Aufgabe 6: Wegen der Kommutativität \( A \cdot B=B \cdot A \) muss gelten:
$$ \begin{array}{l} \left(\begin{array}{ll} x & y \\ z & w \end{array}\right) \cdot\left(\begin{array}{ll} 1 & 1 \\ 0 & 1 \end{array}\right)=\left(\begin{array}{cc} 1 & 1 \\ 0 & 1 \end{array}\right) \cdot\left(\begin{array}{cc} x & y \\ z & w \end{array}\right) \Rightarrow \\ \left(\begin{array}{ll} x & x+y \\ z & z+w \end{array}\right)=\left(\begin{array}{cc} x+z & y+w \\ z & w \end{array}\right) \end{array} $$
Hieraus folgt unter anderem \( x+y=y+w \) und \( z+w=w \). Dies bedeutet \( x=w \) und \( z=0 \). Somit haben alle Matrizen, die zu
$$ \left(\begin{array}{ll} 1 & 1 \\ 0 & 1 \end{array}\right) $$
kommutativ sind die Gestalt
$$ \left(\begin{array}{cc} w & y \\ 0 & w \end{array}\right) . $$
Was wurde hier gemacht? Wieso folgt aus
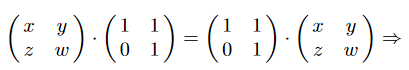
Text erkannt:
\( \left(\begin{array}{cc}x & y \\ z & w\end{array}\right) \cdot\left(\begin{array}{ll}1 & 1 \\ 0 & 1\end{array}\right)=\left(\begin{array}{ll}1 & 1 \\ 0 & 1\end{array}\right) \cdot\left(\begin{array}{cc}x & y \\ z & w\end{array}\right) \Rightarrow \)
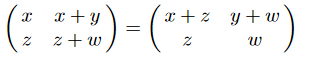
Text erkannt:
\( \left(\begin{array}{cc}x & x+y \\ z & z+w\end{array}\right)=\left(\begin{array}{cc}x+z & y+w \\ z & w\end{array}\right) \)
Und wie kann man daraus das Ergebnis ableiten??
Vielen Dank im Voraus!