Aufgabe:
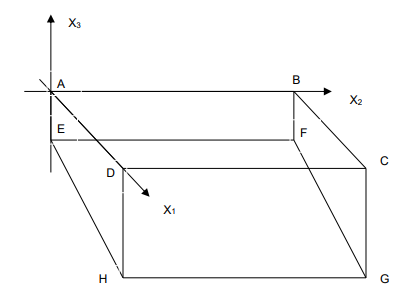
In einem Garten wurde ein Teich nach der unten gezeigten Skizze angelegt. Die Kante AB ist 5 m und die Kante AD 4m lang. Die Tiefe beträgt im Punkt E 1m und im Punkt H 2m.
i) Ein runder Strahler soll so unterhalb der Wasseroberfläche angebracht werden, dass sein Mittelpunkt M die Koordinaten (2/1/-0,5) hat. Berechnen Sie den Abstand des Strahlers vom Boden des Teichs.
ii) Vom Punkt M strahlt das Licht geradlinig in Richtung des Vektors \( \vec{u} \)\( \begin{pmatrix} 1\\5\\2 \end{pmatrix} \). Überprüfen Sie rechnerisch, ob dieser Lichtstrahl eine im Garten im Punkt P(3/6/0) aufgestellte 2m hohe Statue trifft. (Die Lichtbrechung und die Breite der Statue bleiben unberücksichtigt)
iii) Ein Wasserspeier wurde so am Rand des Teichs aufgestellt, dass er vom Punkt W(0/0/0,5) aus einen parabelförmigen Wasserstrahl abgibt, der genau in der x2-x3-Ebene liegt und durch die Gleichung x3=-\( \frac{1}{3} \) x2 ^2+x2+0,5 beschrieben werden kann. Bestimme den Abstand des höchsten Punktes dieses Wasserstrahls vom Beckenrand AB.
Problem/Ansatz:
A(0/0/0); B(0/5/0); C(4/5/0); D(4/0/0); E(0/0/-1); F(0/5/-1); G(4/5/-2); H(4/0/-2)
i) hätte ich den Abstand vom Punkt M zur Ebene E1 bestimmt, welche mit den Punkten E,F,G und H festgelegt wird.
ii) hier hätte ich die Geradengleichung des Lichtstrahls gebildet, wobei M der Stützvektor ist und \( \vec{u} \) der Richtungsvektor. Dann hätte ich eine Punktprobe mit dem Punkt P(3/6/2) durchgeführt.
iii) hier würde ich das Maximum der quadratischen Funktion bestimmen. Dann die Geradengleichung AB bestimmen. Abschließend dann den Abstand vom Maximum zur Geraden AB berechnen.
Sind meine Punkte A-H und meine Ansätze richtig? Vielen Dank im voraus.