Vektor Geraden im Raum

Question

Aufgabe:

(b) Zeichnen Sie die Punkte Q $(3|-2| 1)$ und $\mathrm{T}(0|5| 2)$ in das folgende Koordinatensystem ein. Zeichnen Sie außerdem die Gerade h ein, die durch $\mathrm{Q}$ und $\mathrm{T}$ verläuft.

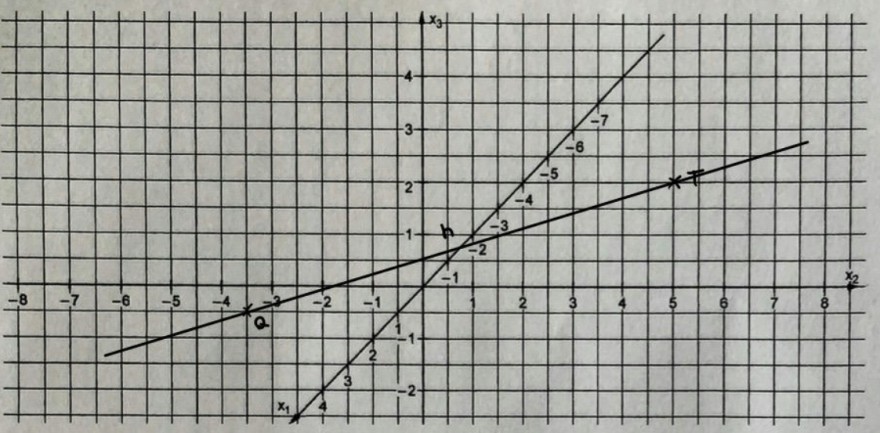
(Schrägbild mit Y nach rechts und X nach links unten. Y-Koordinate von -8 bis 8 und Z-Koordinate von -3 bis 5)

(c) Die Geradengleichung von $h$ lautet $h: \vec{x}=\left(\begin{array}{l}2 \\ 4 \\ 3\end{array}\right)+r \cdot\left(\begin{array}{l}3 \\ 3 \\ 1\end{array}\right), r \in \mathbb{R}$. Beschreiben Sie anhand der
Punkte $Q$ und $T$ wie diese Geradegleichung entsteht und vervollständigen Sie anschließend den Merkkasten.

(der Merkkasten)

Die Geradengleichung einer Geraden $g$, die durch $\mathrm{A}\left(a_{1}\left|a_{2}\right| a_{3}\right)$ und $\mathrm{B}\left(b_{1}\left|b_{2}\right| b_{3}\right)$ verläuft, lautet$$g_{A B}: \vec{x}=\begin{pmatrix} {}\\ {\quad}\\ {}\end{pmatrix}+r \cdot\begin{pmatrix} {}\\ {\quad}\\ {}\end{pmatrix}, \quad r \in \mathbb{R}$$

(d) Beschreiben Sie, wie man mit Hilfe der Geradengleichung von $h$, verschiedene Punkte berechnen kann, die auf der Geraden $h$ liegen. Geben Sie mindestens vier Punkte auf $h$ an.

(e) Prüfen Sie rechnerisch mit Hilfe der Punktprobe, ob die Punkte $B_{1}\left(\frac{3}{4}|3| \frac{7}{4}\right), \quad B_{2}(21|-44|-5)$, $B_{3}(-27|68| 10)$ auf $h$ liegen.

Comments

kann mir jemand bitte helfen

---

Infos über Geraden im Raum und die Ebenengleichungen

Text erkannt:

Gerade is
Homeseparaneter wird $\mathrm{r}=1$ gesetzt
Bleichgesetat ergibt: (bx/by/bz)-(ax/ay/a $-8 i c h t u n g: b x=a x+1 * m x e r_{B}+a t=$
$: A(a \times / a y / a z) \sin A d x$
$8(B x / b y / b z)$ sind die $x, y$ und $z$ koordinaten dei
Abstand von 2 punkten in Raun Hfer ist der "Betrag" von d 21 $(3-v)^{2}+1$
$S_{k} a \operatorname{lar} p r o d u k t \quad a^{*} b-a x^{*} b x+a y^{*} b y+a z^{*} b z$
stehen die beiden Vektoren a und das Skalarprodukt gleich NULL $1 !$ Wsenkrecht" aufeinander,so ist
$-180-a^{*} b-a x^{*} b x+a y^{*} b y+a z^{*} b z=0$
Zbenen Dreipunktgleichung der Zben $t \ldots$
segeben sind die 3 Punkte $a(\mathrm{ax} / \mathrm{ay} / \mathrm{az})$ und $\mathrm{b}(\mathrm{b} \mathrm{x} / \mathrm{by} / \mathrm{bz})$ und $\mathrm{c}(\mathrm{cx} / \mathrm{c} \mathrm{y}$
$c(c x / c y / c z)$
$1 \mathrm{t}\left(\overrightarrow{6}+\vec{b}-\vec{a}^{b}\right)$ und $\vec{v}=(\vec{c}-\overrightarrow{8})$
Normalengleichung der Ebene $\mathrm{E}:(\vec{x}-\vec{a})=\overrightarrow{\vec{d}}=0 \quad \mathrm{n}(\mathrm{nx} / \mathrm{ng} / \mathrm{nz})$ -Nornalen
Der Normalenvektor steht "senkrecht" auf den Richt unesvelen
Koordinatengleichung der Bbene $\mathrm{E}: \mathrm{a}^{+} \mathrm{x}+\mathrm{b}^{*} \mathrm{y}+\mathrm{c}^{*} \mathrm{z}+\mathrm{d}=0$
$\underline{\text { Vektorprodukt (Kreuzprodukt) }}$
Hiermit kann man den "Normalenvektor" fur die Bbene bestingen

---

wie kann ich h rausbekommen =?

---

wie kann ich h rausbekommen =?

$h$ ist bereits in der Aufgabenstellung gegeben:

"Die Geradengleichung von $h$ lautet $h: \vec{x}=\left(\begin{array}{l}2 \\ 4 \\ 3\end{array}\right)+r \cdot\left(\begin{array}{l}3 \\ 3 \\ 1\end{array}\right), r \in \mathbb{R}$."

---

Ja aber wie zeiche ich das denn =?

---

Dazu muß man natürlich ein 3-d-Bild (Schrägbild) zeichnen können.

Tipp:Nimm eine Milchtüte und betrachte diese.

Dann zeichnest du alle sichbaren Kanten auf ein DIN A4 Blatt,wie du sie sieht.

Die unsichbaren Kannten zeichnest di als gestrichelte Linien.

Achte darauf,dass da Seiten parallel liegen.

Mehr kann ich dir auch nicht helfen.

Buchtipp:

Mathematik Analytische Geometrie/Stochastik Band 2

Cornelsenverlag

Bestell-Nr.:ISBN 978-3-06-000479-9

Hat mir damals 45 € gekostet mit Lösungsbuch

Eignet sich zum Selbstudium.Hat 423 Seiten mit Formeln,Zeichnungen und durchgerechneten Beispielaufgaben.

Da siehst du auch Schrägbilder.Die Maße kannst du dann da ausmessen.

---

ich hatte die zwei Vektoren eingetragen und einfach miteinander verbunden

---

Können wir die Aufgaben zusammen machen ? bei c) habe ich schon folgendes:

x= (ax,ay,az)+r*(bx-ax,by-ay,bz-az)

bei d) habe ich dass die Geradengleichung eine Punktschar in Abhängigkeit von r ist und durch das einsetzen der Werte kann man die Aufgabe abschließen

Answer 1

(b) Zeichnen Sie die Punkte Q $(3|-2| 1)$ und $\mathrm{T}(0|5| 2)$ in das folgende Koordinatensystem ein. Zeichnen Sie außerdem die Gerade h ein, die durch $\mathrm{Q}$ und $\mathrm{T}$ verläuft.

Das hast du richtig gemacht.

(c) Die Geradengleichung von $h$ lautet

$h: \vec{x}=\left(\begin{array}{l}2 \\ 4 \\ 3\end{array}\right)+r \cdot\left(\begin{array}{l}3 \\ 3 \\ 1\end{array}\right), r \in \mathbb{R}$

Nein, das tut sie nicht.

c) habe ich schon folgendes: x= (ax,ay,az)+r*(bx-ax,by-ay,bz-az)

Das ist richtig.

wie man mit Hilfe der Geradengleichung von $h$, verschiedene Punkte berechnen kann, die auf der Geraden $h$ liegen.

Man setzt verschiedene Werte für den Parameter ein.

(e) Prüfen Sie rechnerisch mit Hilfe der Punktprobe, ob die Punkte $B_{1}\left(\frac{3}{4}|3| \frac{7}{4}\right), \quad B_{2}(21|-44|-5)$, $B_{3}(-27|68| 10)$ auf $h$ liegen.

Setze den Ortsvektor des Punktes, den du prüfen möchtest, für $\vec{x}$ in die Geradengleichung ein. Der Punkt liegt genau dann auf der Geraden, wenn die so entstandene Gleichung eine Lösung hat.