Hallo Clara,
Deine Frage hatte ich übersehen. Aber eine späte Antwort ist besser als gar keine:
Jeder Kreis, dessen Durchmesser eine der Seiten des Dreiecks ist, geht auch durch zwei Höhenfußpunkte.
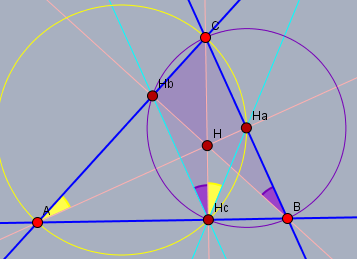
Somit sind die Winkel \(\angle CH_cH_b\) und \(\angle CBH_b\) (lila) Peripheriewinkel im lila Kreis über der Sehne \(H_bC\) und \(\angle H_aH_cC\) und \(\angle H_aAC\) (gelb) im gelben Kreis über der Sehne \(CH_a\) jeweils paarweise gleich groß.
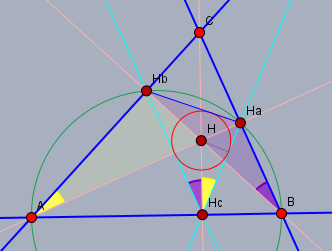
Im dritten Kreis (grün) sind die Winkel \(\angle H_aAH_b\) (gelb) und \(\angle H_aBH_b\) (lila) Peripheriewinkel über der Sehne \(H_aH_b\) und somit ebenfalls gleich groß.
Daraus folgt, dass alle vier Winkel gleich groß sind und jede Höhe auch Winkelhalbierende des Winkels ist, der durch die beiden Geraden (hellblau) durch den Höhenfußpunkt der jeweiligen Höhe (hier \(H_c\)) zu den beiden anderen Höhenfußpunkten gebildet wird. Die Höhen schneiden sich in einem Punkt \(H\) und somit ist \(H\) auch Schnittpunkt der Winkelhalbierenden im Dreieck \(\triangle H_aH_bH_c\) und Mittelpunkt der Inkreises in \(\triangle H_aH_bH_c\).
Gruß Werner