Wie teilt M die Strecke LN?

Question

ABC sei ein gleichseitiges Dreieck mit den Mitten L und M zweier Seiten. Die Gerade LM schneidet den Umkreis von ABC insbesondere in N, sodass M auf \( \overline{LN} \) liegt. Wie teilt M die Strecke \( \overline{LN} \)?

Comments

Wie teilt M die Strecke \( \overline{LN} \)?

Duplikat :  In welchem Verhältnis teilt F die Strecke \( \overline{CD} \)?

---

Ich verstehe: Zwei Aufgaben mit dem gleichen Ergebnis sind bei Gast hj2166 identisch.

Answer 1

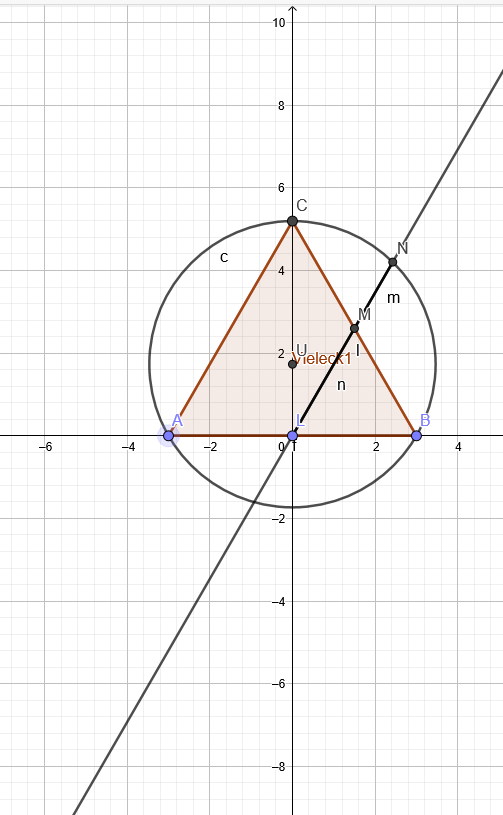
ABC sei ein gleichseitiges Dreieck mit den Mitten L
und M zweier Seiten. Die Gerade LM schneidet den Umkreis von ABC insbesondere in N, sodass M auf \( \overline{LN} \) liegt. Wie teilt M die Strecke \( \overline{LN} \)?

Dreieck A,B, C mit A(-\( \frac{c}{2} \)|0) , B( (\( \frac{c}{2} \)|0)  C(0|\( \frac{c}{2} \)•\( \sqrt{3} \))
L(0|0) und M (\( \frac{c}{4} \)|\( \frac{c}{4} \)•\( \sqrt{3} \))
Gerade durch L und M:     y=\( \sqrt{3} \)•x
Kreis um U(0|\( \frac{c}{6} \)•\( \sqrt{3} \))
\( x^{2} \)+(y-\( \frac{c}{6} \)•\( \sqrt{3} \))^2= \( \frac{1}{3} \)\( c^{2} \) geschnitten mit y=\( \sqrt{3} \)•x
Koordinaten von N:
\( x^{2} \)+(\( \sqrt{3} \)•x-\( \frac{c}{6} \)•\( \sqrt{3} \))^2= \( \frac{1}{3} \)\( c^{2} \)
x₁=\( \frac{c}{8} \)+\( \frac{c}{8} \)•\( \sqrt{5} \)
y₁=(\( \frac{c}{8} \)+\( \frac{c}{8} \)•\( \sqrt{5} \))•\( \sqrt{3} \)
\( \overline{LN} \): \( \frac{c}{4} \)•(1+\( \sqrt{5} \))

\( \overline{LM} \):\( \frac{c}{2} \)

 \( \overline{MN} \): \( \frac{c}{4} \)•(1+\( \sqrt{5} \))-\( \frac{c}{2} \)= \( \frac{c}{4} \)+\( \frac{c}{4} \)\( \sqrt{5} \)-\( \frac{c}{2} \)=\( \frac{c}{4} \)\( \sqrt{5} \)- \( \frac{c}{4} \)= \( \frac{c}{4} \)•(\( \sqrt{5} \)-1)

\( \overline{MN} \):\( \overline{LM} \)=\( \frac{c}{4} \)•(\( \sqrt{5} \)-1):\( \frac{c}{2} \)=\( \frac{1}{2} \)•(\( \sqrt{5} \)-1)≈0,618