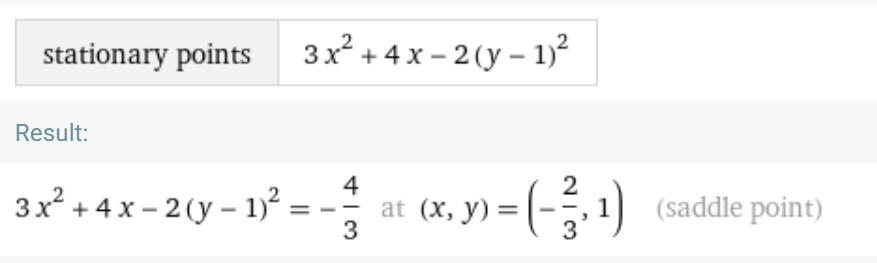Minima, Maxima und Sattelpunkt bestimmen

Question

Aufgabe:

f(x,y)=3x^2+4x-2(y-1)^2
Problem/Ansatz:

die Funktion Minima, Maxima und Sattelpunkte.

vielen dank

ivan

Comments

Leite nach x und nach y ab!

Sattelpunkt: f '(x,y)= 0, f ''(x,y) = 0

---

vielen dank:)

Answer 1

Hallo,

1.)fx , fy , fxy, fyx, fyy ,fxx bilden

fx=6x+4

fy= -4y+4

fxx=6

fyy= -4

fxy=fyx=0

2.) Hesse Matrix aufstellen

\( H_{f}(x, y)=\left(\begin{array}{ll}f_{x x} & f_{x y} \\ f_{y x} & f_{y y}\end{array}\right) \)

\( H_{f}(x, y)=\left(\begin{array}{ll}{6} & {0} \\ {0} & {-4}\end{array}\right) \)

3.) Extremstellen berechnen

fx=6x+4=0 --->x=-2/3

fy= -4y+4=0 ---->y=1

4.) Extrempunkte in die Hessematrix einsetzen

\( H_{f}(x, y)=\left(\begin{array}{ll}{6- λ} & {0} \\ {0} & {-4-λ}\end{array}\right) \)

λ₁=4

λ₂= -6 -->Sattelpunkt

5.) neg .und positiver Eigenwert ->Sattelpunkt

beide Eigenwerte positiv ---->Minimum

beide Eigenwerte negativ --->Maximum

Comments

Vielen Dank für die hilfreiche Antwort, hatte später die gleiche Lösung, war mir aber immer noch nicht sicher, danke nochmal:)