Aufgabe 1:
Über zwei benachbarten Seiten in einem regelmäßigen Sechseck bzw. Achteck werden nach innen Quadrate gezeichnet, die sich in einer Drachenfigur überschneiden. Bestimme jeweils den Flächeninhalt des Inkreises des Drachens für die Seitenlängen \( a=\overline{A B}=6 \) LE. des Sechsecks bzw. \( a=\overline{A B}=4 \) LE des Achtecks.
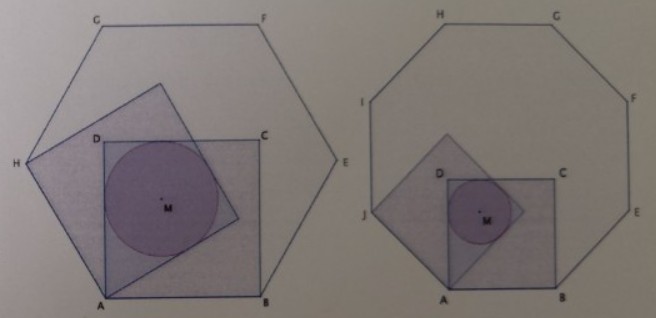
Gib einen allgemeinen Term für den Radius \( r_{n}, n \geq 3 \) des Inkreises an, den man auf diese Weise für ein regelmäßiges \( n \)-Eck mit der Seitenlänge \( a \) erhält und verdeutliche damit, dass \( \lim \limits_{n \rightarrow \infty} r_{n}=0 \).
Aufgabe 2:
Bestimme die Lösung der Gleichung \( \sqrt[3]{x+3}=\sqrt{x-1} \) und zeige, dass diese Lösung eindeutig ist.