Hallo Sterni,
Jede Parabel lässt sich in der Form $$y = \frac1{4f}(x-x_s)^2 + y_s$$schreiben. Wobei der Punkt \(S(x_s|\,y_s)\) der Scheitel und \(f\) die Brennweite ist. Die Koordinaten des Scheitels kann man aus der Funktionsgleichung ablesen \(S(-3|\,0)\). \(f\) ist gleichzeitig der (vertikale) Abstand des Brennpunkts \(F\) vom Scheitelpunkt \(S\). \(f\) berechnet sich hier aus$$\frac 1{4f} = 1 \implies f = 0,25$$
Um den \(x\)-Wert für \(y=4\) graphisch zu bestimmen, zeichne zunächst den Scheitelpunkt \(S(-3|\,0)\) und die Senkrechte (rot) durch \(S\) in ein Koordinatensystem ein. Markiere auf der Senkrechten den gewünschten Punkt \(Y\) bei \(y=4\).
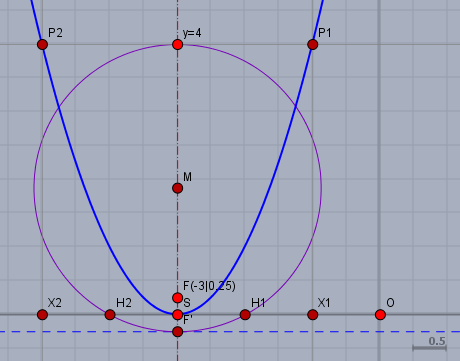
Dann trage den Brennpunkt ein, der in diesem Fall bei \(F(-3|\,0,25)\) liegt (\(|SF|=f\)). Dann spiegele den Brennpunkt \(F\) an \(S\). Man erhält \(F'(-3|\,-0,25)\). Konstruiere den Mittelpunkt \(M\) der Strecke \(F'Y\) und zeichne den Kreis (lila) um \(M\) mit Radius \(MF'\). Dieser Kreis schneidet die Waagerechte durch \(S\) - in diesem Fall ist das die X-Achse - in den Punkten \(H_1\) und \(H_2\).
Dann spiegele den Scheitel \(S\) einmal am Punkt \(H_1\) und einmal an \(H_2\). Du erhältst die Punkte \(X_1(-1|\,0)\) und \(X_2(-5|\,0)\). Dies sind die gesuchten X-Koordinaten bei denen die Funktion den Wert \(y=4\) annimmt.
Gruß Werner