Zeige: Die Radien von Kp und Kq sind gleich.

Question

C sei ein beliebiger Punkt auf der Strecke AB. K₁ sei ein Kreis um M₁ mit dem Durchmesser AC. K₂ sei ein Kreis um M₂ mit dem Durchmesser CB. s₁ und t₁ seien Tangenten durch A an K₂. s₂ und t₂ seien Tangenten durch B an K₁. K_p sei ein Kreis durch C mit den Tangenten s₁ und t₁ und dem Radius p. K_q sei ein Kreis durch C mit den Tangenten s₂ und t₂ und dem Radius q. Zeige p=q.

Comments

Der Strahlensatz

a / q   =   (2b+a) / (2b - q)   zeigt, dass   q = ab / (a+b)  symmetrisch in a und b ist.

Apropos "Symmetrie" : würdest du mir meine Frage in https://www.mathelounge.de/873950/zeigen-sie-dass-r-eine-aquivalenzr… an dich beantworten ?

Answer 1

Hallo Roland,

folgende Lösung ist ähnlich zu der von hj, aber IMHO nicht identisch.

Man findet in der Figur zwei Paare von ähnlichen Drachenvierecken:

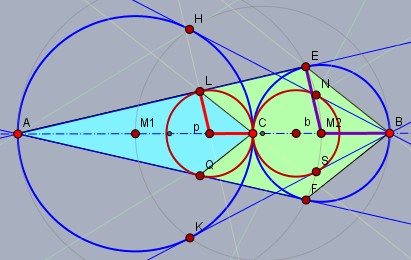
Eines der Paare sind die beiden Drachenvierecke $AQCL$ (hellblau) und $AFBE$ (grün). Diese sind ähnlich, da sie sich aus ähnlichen Dreiecken zusammen setzen lassen. Folglich sind alle Streckenverhältnisse in beiden Vierecken identisch.

Also auch das Verhältnis des Radius ($p$ und $b$) des Umkreises ($K_p$ und $K_2$) der rechten drei Eckpunkte zur halben horizontalen Diagonalen ($a$ und $a+b$):$$\frac{p}{a}=\frac{b}{a+b} \implies p = \frac{ab}{a+b}$$Und da dieser Tem invariant gegenüber dem Vertauschen von $a$ und $b$ ist, gilt das auch für den Radius $q$.

Der Kreisdurchmesser von $K_p$ (bzw. $K_q$) ist somit das harmonische Mittel der Radien $a$ und $b$.

Gruß Werner