Aufgabe:
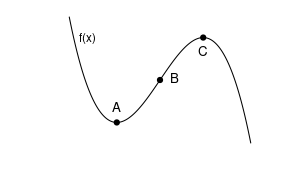
Die folgende Grafik zeigt drei kritische Punkte der Funktion f(x) bzw. ihrer Ableitung f′(x). Die Funktion ist gegeben durch:
f(x)=−0.39x^3+0.66x^2+1.04x+1.34
Problem/Ansatz:
Welchen Wert hat die zweite Ableitung f′′(x) im Punkt A?
Mein Ergebnis ist -2,34x + 1,32, ist das richtig?