Vom Duplikat:
Titel: Bestimmen Sie die Wahrscheinlichkeit graphisch
Stichworte: graphisch,normalverteilung,stochastik
Aufgabe: Die Abb. zeigt den Graph einer normalverteilten Zufallsgröße X.
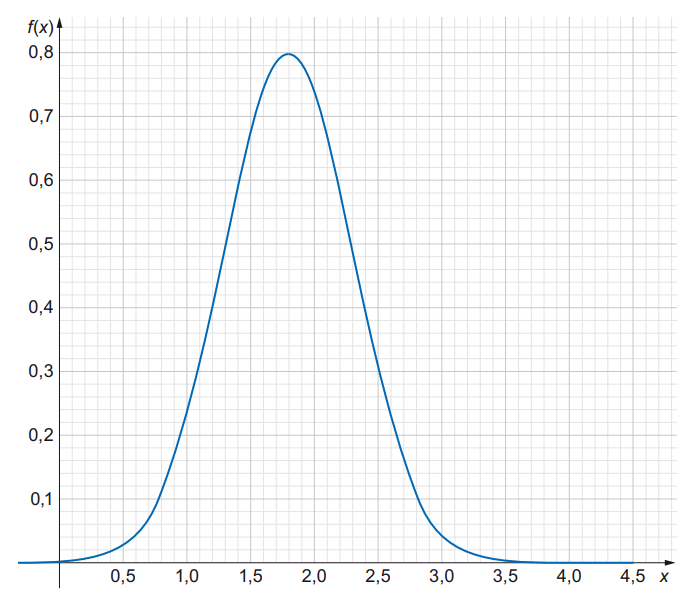
a) Geben Sie den Erwartungswert der Zufallsgröße an.
b) Geben Sie die Wahrscheinlichkeit für X = 1,2 an.
c) Bestimmen Sie die Wahrscheinlichkeit dafür, dass X einen Wert aus dem Intervall [2,1; 2,6] annimmt.
Problem/Ansatz:
Erwartungswert = 1.8, da an der Stelle x = 1.8 der Hochpunkt ist.
Wie kann man (ohne Taschenrechner und ohne Tools) die Wahrscheinlichkeit für X graphisch bestimmen?