Gegeben ist folgende Aufgabe:

1. Frage: Wieso ist k5 = 1? War das nicht so, dass alle Spalten zusammenaddiert 1 ergab? Aber laut den Lösungen ist k5 alleine schon 1.
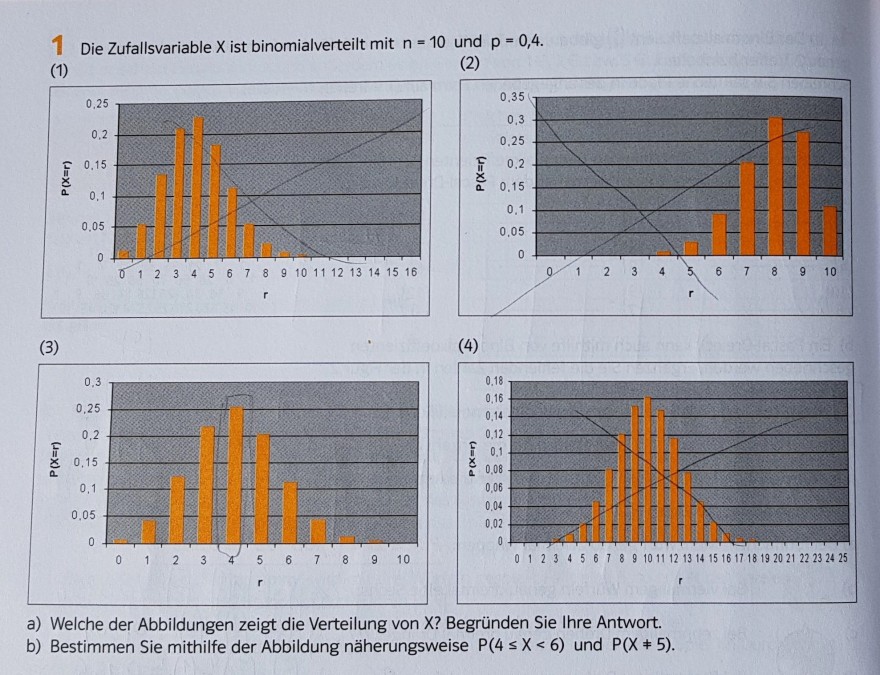
2. Frage: Ich soll die Wahrscheinlichkeit dafür berechnen, dass X den Wert 2 annimmt. So eine ähnliche Aufgabe hatten wir bereits in der Schule gemacht (siehe Bild unten). Warum ist das hier anders? Also, konkreter: In der Schule sollten wir mithilfe der Abbildung näherungsweise P(4<=X<6) berechnen. Um das zu berechnen, muss man folgendes tun: P(X=4) + P(X=5) = 0,45 (siehe Abbildung unten)
Auf die obige Aufgabe bezogen jedoch, muss man folgendes tun, damit X den Wert 2 annimmt: P(X=2) = P(X<=2) - P(X<=1) = 0,3.
Wieso ist das anders? Beides sind doch die gleichen Aufgaben, nur mit anderen Werten, oder nicht??