Potenzen und Wurzeln

Question

Aufgabe:

Logarithmus

Problem/Ansatz : Ich denke das die 3,3598 nicht stimmt aber ich bin mir nicht sicher kann mir jemand bitte helfen danke :)

Text erkannt:

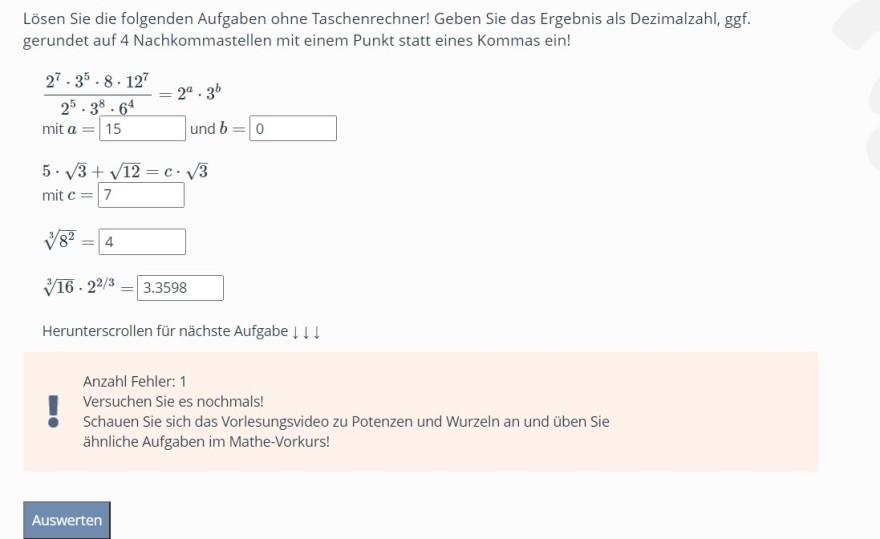
Lösen Sie die folgenden Aufgaben ohne Taschenrechner! Geben Sie das Ergebnis als Dezimalzahl, ggf. gerundet auf 4 Nachkommastellen mit einem Punkt statt eines Kommas ein!
$\frac{2^{7} \cdot 3^{5} \cdot 8 \cdot 12^{7}}{2^{5} \cdot 3^{8} \cdot 6^{4}}=2^{a} \cdot 3^{b}$
mit $a=15 \quad$ und $b=0$
$5 \cdot \sqrt{3}+\sqrt{12}=c \cdot \sqrt{3}$
mit $c=7$
$\begin{array}{l} \sqrt[3]{8^{2}}=4 \\ \sqrt[3]{16} \cdot 2^{2 / 3}=3.3598 \end{array}$
Herunterscrollen für nächste Aufgabe $\downarrow \downarrow \downarrow$
Anzahl Fehler: 1
Versuchen Sie es nochmals!
Schauen Sie sich das Vorlesungsvideo zu Potenzen und Wurzeln an und üben Sie ähnliche Aufgaben im Mathe-Vorkurs!
Auswerten

Comments

Was hat das mit Logarithmus zu tun?

Answer 1

$2^{4/3}·2^{2/3}$ solltest du nochmal nachrechnen.

Answer 2

Umwandeln, zusammenfassen und kürzen, Potenzgesetze anwenden

8= 2³

12= 2²*3 -> 12⁷ = 2¹⁴*3⁷

6⁴ = (2*3)⁴ = 2⁴*3⁴

√12 = 2*√3

3. Wurzel aus 8² = 8^(2/3) = 2^(6/3) = 2² = 4

3. Wurzel aus 16 = 16^(1/3) = 2^(4/3)

Answer 3

$\sqrt[3]{16} \cdot 2^{2 / 3}\\=\sqrt[3]{2^4} \cdot \sqrt[3]{2^2} = \sqrt[3]{2^6}=2^2=4$