Da 1 ursprünglich ausgeschlossen wurde im Definitionsbereich heißt das, dass für die Funktion ƒ(2) = 1 gleich gelten …

Question

Aufgabe:

Man überlege, wie die Parameter a und b (∈ ℝ) zu wählen sind, damit die Funktion ƒ: ℝ∖ {4;1;5} →ℝ, mit

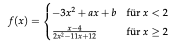
Text erkannt:

\( f(x)=\left\{\begin{array}{ll}-3 x^{2}+a x+b & \text { für } x<2 \\ \frac{x-4}{2 x^{2}-11 x+12} & \text { für } x \geq 2\end{array}\right. \)

in x₀ = 2 stetig ist.

Problem/Ansatz:

In den Lösungen steht, das für b gilt: b = 12 - 2a

Meine Frage jetzt ich erhalte grunsätzlich für den rechtsseitigen Grenzwert von ƒ(2) = 1;

aber in dem Fall ware b = 13 - 2a.

Da 1 ursprünglich ausgeschlossen wurde im Definitionsbereich heißt das, dass für die Funktion ƒ(2) = 1 gleich gelten muss ƒ(2) = 0?

Oder bin ich falsch an die Aufgabe rangegangen und habe das falsch berechnet?

Answer 1

Der linksseitige Grenzwert ist doch -12+2a+b

und das muss =1 sein   -12+2a+b = 1

Da bekomme ich auch b = 13-2a

Comments

Genau deshalb bin ich gerade etwas überfragt, warum in den Lösungen b = 12 - 2a steht. Und da in der Aufgabenstellung bereits erwähnt wurde, das der Definitionsbereich dem Mengenbereich der reellen Zahlen, ausgeschlossen 4, 1 und 5, entspricht. aber f(2) = 1 würde ja dann doch eigentlich zu dem Wertebereich gehören. Dann müssen die Lösungen falsch sein

---

Dann stimmt die "Lösung" nicht. Habe nämlich dasselbe.