Aufgabe:
Benutzen Sie die folgende (hier nicht beweisen, aber relativ leicht einzusehende) Beziehung für die RencontresZahlen:
Dn =(n-1) . (Dn-1 + Dn-2 ) (*).
Zeigen Sie also mit Hilfe von (*), dass für alle n ∈ N gilt:
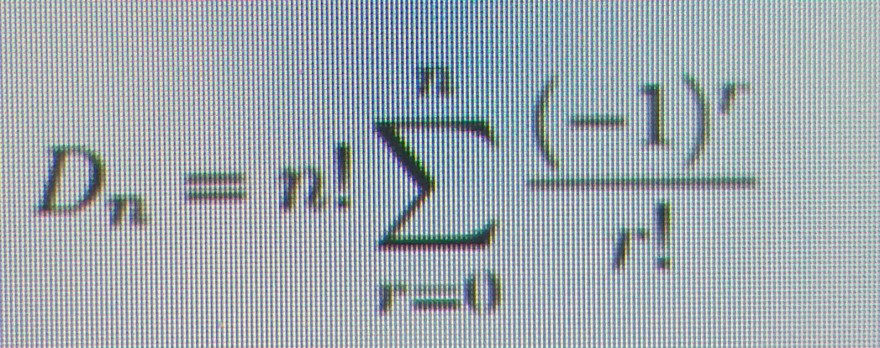
Text erkannt:
\( D_{n}=n ! \sum \limits_{r=0}^{n} \frac{(-1)^{r}}{r !} \)
(Hinweis: Es ist D0 = 1 und D1 = 0. Beachten Sie, dass (*) wegen des Faktors (n - 1) auch für n =1 gültig ist, egal wie wir D-1 definieren würden. Betrachten Sie dann zunächste die Zahlen
An = Dn -nDn-1 (**)
und zeigen, dass An = (-1)n gilt. Teilen Sie dann beide Seiten von (**) durch n! und schließen Sie daraus auf die Behauptung.)
Ich BITTE BITTE Sie, dass Sie mir bei dieser Frage helfen. Ich kann die Aufgabe nicht lösen :"(