Aufgabe:
Ich habe folgende Aufgabe:
\( \int \limits_{1}^{3} \frac{1}{3 x^{\frac{2}{3}}} d x \)
Problem/Ansatz:
Ich weiss man könnte einfach 1/3 ausklammern. Ich möchte es jedoch mit der Substitutions-Methode lösen. Ich weiss jedoch nicht genau was ich falsch mache. Kann mir hier jemand den Fehler aufzeigen?
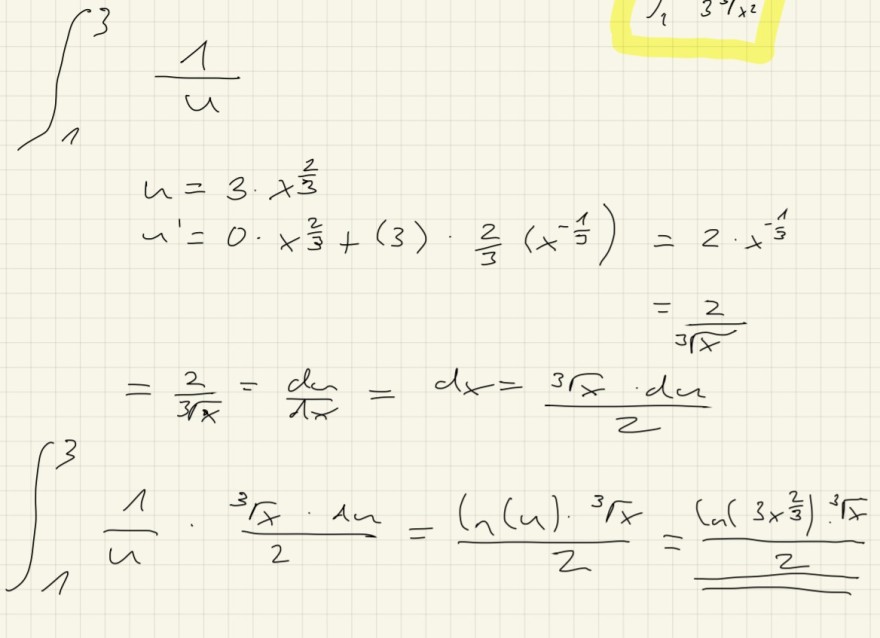
Text erkannt:
\( \int \limits_{1}^{3} \frac{1}{4} \)
\( u=3 \cdot x^{\frac{2}{3}} \)
\( u^{\prime}=0 \cdot x^{\frac{2}{3}}+(3) \cdot \frac{2}{3}\left(x^{-\frac{1}{3}}\right)=2 \cdot x^{-\frac{1}{3}} \)
\( =\frac{2}{\sqrt[3]{x}} \)
\( =\frac{2}{\sqrt[3]{x}}=\frac{d x}{d x}=d x=\frac{3 \sqrt{x} \cdot d x}{2} \)
\( \int \limits_{1}^{3} \frac{1}{4} \cdot \frac{\sqrt[3]{x} \cdot \ln }{2}=\frac{\ln (u) \cdot \sqrt[3]{x}}{2}=\frac{\ln \left(3 x^{\frac{2}{3}}\right) \sqrt[3]{x}}{2} \)
Vielen Dank im Voraus!