Hallo Zahri,
das ist 'ne ziemlich gute Frage! Wo sind eigentlich die Fluchtpunkte?
Die Positionen der Fluchtpunkte hängen davon ab, wo der Beobachter steht, wohin er sieht und welchem Winkel das Objekt zu ihm steht, auf das er sieht. Um das zu verstehen ist es notwendig, sich das ganze Szenario im Dreidimensionalen - also räumlich - vorzustellen. Dazu habe ich Dir ein Beispiel in Geoknecht3D eingegeben.
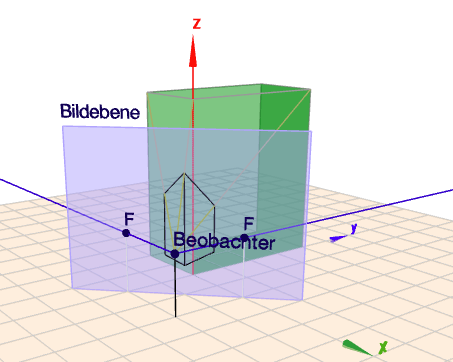
Klicke bitte auf obiges Bild. Dann öffnet sich Geoknecht3D und Du kannst die Szene mit der Maus rotieren, um Dir einen räumliche Eindruck der Szene zu verschaffen.
Dort siehst Du den Beobachter, der auf einen grünen Quader sieht. Im Quader stehen alle Kanten parallel oder senkrecht zu einander. Im Bild (auf der Bildebene) ist dies aber nicht mehr der Fall. Dieses Bild, welches der Beobachter sieht, habe ich auf die Bildeben gezeichnet.
Durch die Perspektive (das ist eine sogenannte Zentralperspektive) wird das Bild des Quaders 'verzerrt'. Parallele Kanten, die nicht parallel zur Bildebene verlaufen, schneiden sich in Fluchtpunkten. Und die Fluchtpunkte liegen genau dort wo der Blick des Beobachters parallel(!) zu den jeweiligen Kanten verläuft.
zu Deiner eigentlichen Frage: der "Horizont", auf dem die Fluchtpunkte liegen, liegt etwas tiefer als die Hälfte der Höhe des Quaders, weil der Beobachter auf dieser Höhe steht. Stände er höher, würde auch diese Linie (der Horizont) und mit ihr die Fluchtpunkte nach oben wandern, stände er tiefer, so würde sich der Horizont nach unten verschieben.
Das steht übrigens auch auf dem ersten Bild (oben) aus Deinem Buch:
Augenhöhe = Horizontlinie
Nachtrag:
um das ganze noch mal zu verdeutlichen habe ich Dir eine Szene gebastelt, die von 'oben' so aussieht:
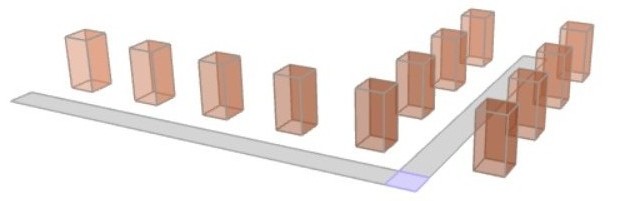
sehe es einfach als ein Straßenzug, an dem quadratische Häuser stehen.
Im nächsten Bild stelle ich den Beobachter in der Nähe des blaue Quadrats im Vordergrund und lasse ihn in den Straßenzug rechts hinein sehen. Das sieht so aus:
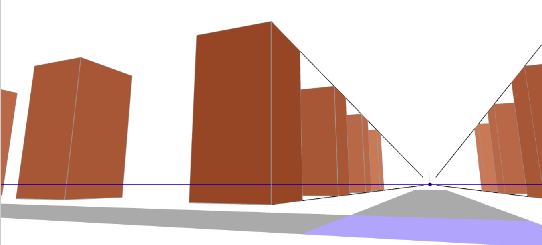
Die 'Häuser' sind größer als der Beobachter und der Beobachter sieht nach oben. Da Horizontline mit Fluchtpunkt auf der Höhe des Beobachters liegt, liegt die Horizontlinie relativ tief.
Jetzt hebe ich den Beobachter an. Er soll jetzt knapp unterhalb der Dachhöhe stehen:
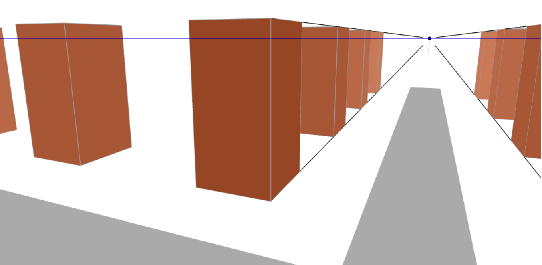
Die Horizonzline rutscht mit dem Beobachter nach oben und die Häuser damit relativ nach unten im Bild.
Noch ein wenig höher gibt dieses Bild:
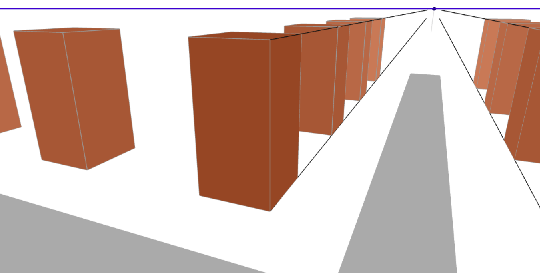
Nun steht der Beobachter so weit oben, dass er von oben auf die Dächer der Häuser sehen kann.
Und nun lasse ich den Beobachter nach links schauen:
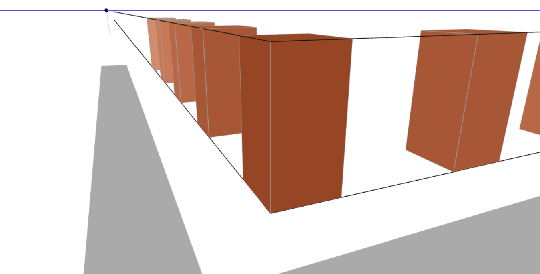
Hier wird der zweite Fluchtpunkt sichtbar.
Damit wollte ich zwei Dinge zeigen:
1. Augenhöhe = Horizontlinie(oben blau eingezeichnet)
2. Die Lage der Fluchtpunkte wird durch die Blickrichtung des Beobachters relativ zum Objekt bestimmt.
Gruß Werner