Hallo döschwo,
die zeichnerische Lösung sagt \(r_1=7,2\,\text{cm}\).
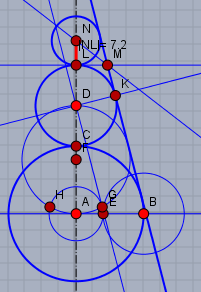
zwei sich berührende Kreise zwischen den gemeinsamen Tangenten sind zu jedem anderen Paar ähnlich. D.h. dass das Verhältnis der Radien zweier benachbarter Kreise stets konstant ist. Also ist$$\frac{r_1}{r_2} = \frac{r_2}{r_3} \implies r_1=\frac{r_2^2}{r_3} = \frac{144}{20}\,\text{cm} = 7,2\,\text{cm}$$Gruß Werner