War heute in meiner Mathe Arbeit, wie rechnet man das?

Question

Aufgabe:

Ein 16cm langer Draht wird zu einem rechtwinkligen Dreieck gelegt. Die kürzeste Seite ist 4cm lang. Wie lange sind die beiden anderen

Problem/Ansatz:

War heute in meiner Mathe Arbeit, wie rechnet man das?

Answer 1

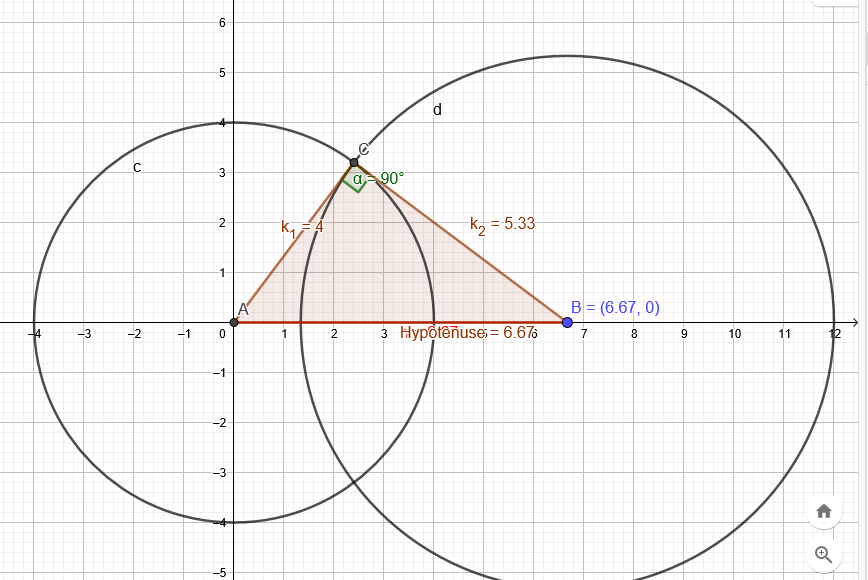
Ein 16cm langer Draht wird zu einem rechtwinkligen Dreieck gelegt. Die kürzeste Seite ist 4cm lang. Wie lange sind die beiden anderen.

Die beiden Katheten:  k₁=4     k₂           die Hypotenuse: h

1.)4+k₂+h=16    1.) h=12-k₂   in 2.) 4^2+k₂^2=(12-k₂) ^2

Pythagoras:

2.) 4^2+k₂^2=h^2

2.) 16+k₂^2=144-24k₂+k₂^2

16=144-24k₂       24k₂=128     k₂ = \( \frac{32}{6} \)     1.) h=12-\( \frac{32}{6} \)=\( \frac{20}{3} \)

Answer 2

4+b+c= 16

c= 12-b

4^2+b^2 = (12-b)^2 = 144-24b+b^2

24b= 128

b= 16/3

c= 20/3

Comments

???? Das verstehe ich jetzt nicht

---

Umfang = a+b+c = 16

a oder b gleich 4 setzen, c = Hypotenuse

4+b+c = 16

Rest über Pythagoras: a^2+b^2= c^2

---

4+b-c = 16 Stimmt das?

---

Danke, Tippfehler. Habs ediert. :)