Steckbriefaufgabe - Sattelpunkt

Question

Aufgabe:

y= x^3+bx^2+cx+d

Sattelpunkt S(1|4)

Ermittle die Funktionsgleichumg von f

Problem/Ansatz:

Ich habe:

f(1)= 4

f‘(1)=0

f‘‘(1)=0

Irgendwie komm ich wieder nicht auf die 4. Bedingung drauf. In der Angabe steht x^3 und nicht ax^3. Hat es etwas damit zu tun?

Answer 1

Benutze http://www.arndt-bruenner.de/mathe/scripts/steckbrief.htm zur Hilfe und Selbstkontrolle.

Eigenschaften

a = 1
f(1) = 4
f'(1)=0
f''(1)=0

Gleichungssystem

a = 1
a + b + c + d = 4
3a + 2b + c = 0
6a + 2b = 0

Errechnete Funktion

f(x) = x^3 - 3·x^2 + 3·x + 3

Answer 2

Ja, denn damit brauchst du nur drei Gleichungen für drei Unbekannte.

Gruß, Silvia

Comments

In den Lösungen steht, dass y= x^3-3x^2+3x+3 rauskommt :/

---

Was stört dich daran?

Answer 3

Hier werden nur drei Bedingungen benötigt.

Answer 4

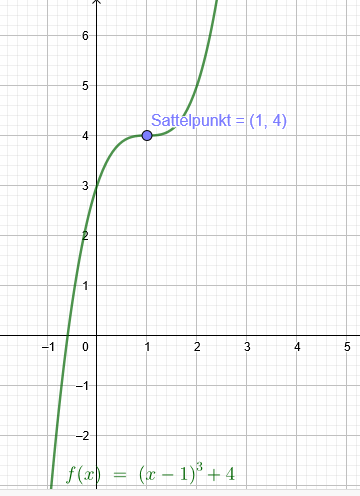
Polynom 3. Grades:

Sattelpunkt S(1|4)

Ich verschiebe den Graphen um 4 Einheiten nach unten:  S´(1|0)

Weiter mit der Nullstellenform der kubischen Parabel .

(Das a fällt weg wegen f(x)=x^3+b x^2+cx +d)

p(x)=(x-1)^3

Nun 4 Einheiten nach oben:

f(x)=(x-1)^3+4