Potenzfunktionen (Extremalwertaufgabe) berechnen?

Question

Aufgabe:

Aus einem quadratischen Stück Pappe der größe 60 cm x 60 cm soll ein oben offener kasten hergestellt werden. Die Ecken mit der variablen Seitenlänge x sind hierzu entsprechend der Abbildung abzuschneiden und die Seiten an den gepunkteten Linien hochzubiegen.

Für welche Höhe x ist das Volumen des Kastens am größten (maximal)?

Problem/Ansatz:

Ich weiß überhaupt nicht wie ich die Aufgabe berechnen soll.

Ich brauche einen ausführlichen Lösungsweg, damit ich es verstehen kann.

Comments

Schon wieder abgemeldet...

Answer 1

1. Formel für das Aufstellen, was extremal werden soll. In deiner Aufgabe soll das Volumen eines Quaders extremal werden:

   (1)        \(V = a\cdot b\cdot c\).

2. Bedingungen formulieren, denen die Variablen der Formel unterliegen.

   Die Ecken mit der variablen Seitenlänge x sind hierzu entsprechend der Abbildung abzuschneiden

   ... und nach oben falten. Eine Seitenlänge des Quaders ist deshalb \(x\):

   (2)        \(a = x\).

   Aus einem quadratischen Stück Pappe der größe 60 cm x 60 cm

   (3)        \(b = 60-2x\)
   

   (4)        \(c = 60-2x\)
   

3. Die Bedingungen verwenden um in (1) Variablen zu eleminieren oder in den Sachzusammenhang einzubetten. Dazu (2), (3) und (4) in (1) einsetzen:

           \(V = x\cdot (60-2x)\cdot (60-2x)\).

   Die Formel kann jetzt als Funktion aufgefasst werden:

   (5)        \(V(x) = x\cdot (60-2x)\cdot (60-2x)\).

   Dabei steht \(x\) für die Seitenlänge der ausgeschnittenen Ecke und \(V(x)\) für das entsprechende Volumen.

4. Für welche Höhe x ist das Volumen des Kastens am größten

   Bestimme den Hochpunkt von \(V(x)\).
   

Die Gleichung (1) heißt Hauptbedingung.

Die Gleichungen (2), (3) und (4) heißen Nebenbedinungen.

Die Gleichung (5) gibt die Zielfunktion an.

Answer 2

Ich nehme an die Skizze sieht so aus

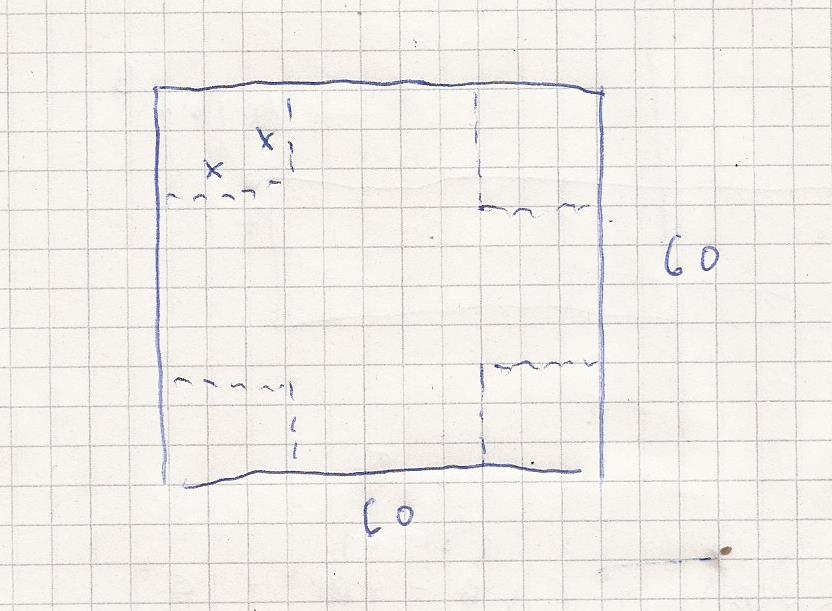
Verbleibende Seitenlänge
60 minus 2 * x

Volumen : Grundfläche mal Höhe
V = ( 60 - 2x ) * ( 60 - 2*x) * x
V = ( 3600 - 240 * x + 4*x^2 ) * x
V = 3600x - 240 * x^2 + 4*x^3
1. Ableitung nach x
V ´( x ) = 3600 - 480 * x + 12 * x^2

Extremwert
3600 - 480 * x + 12 * x^2 = 0
x = 10
und
x = 30 ( Minimum V, entfällt )

x = 10
V = 40 * 40 * 10