wo liegt der Fehler -> pq formel −x^2+x=0

Question

Aufgabe

−x^2+x=0

Wollte diese Aufgabe zusätzlich mittels pq Formel lösen,

jedoch erhalte ich ein anderes Resultat

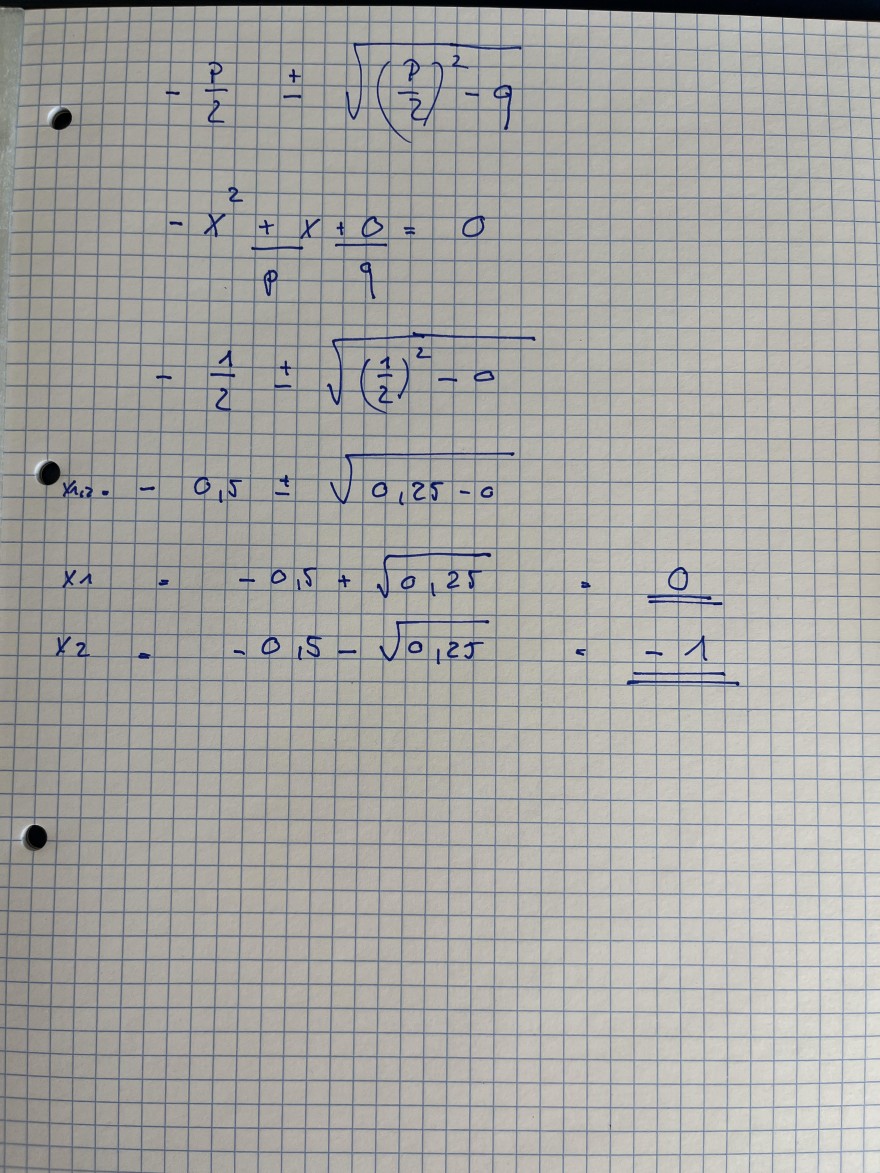
Text erkannt:

\( -\frac{p}{2} \pm \sqrt{\left(\frac{p}{2}\right)^{2}-q} \)
\( -x^{2}+x+\frac{p}{q}=0 \)
\( -\frac{1}{2} \pm \sqrt{\left(\frac{1}{2}\right)^{2}-0} \)
\( x_{x_{12}}-0,5 \pm \sqrt{0,25-0} \)
\( x_{1}=\frac{0,5+\sqrt{0,25}}{x_{2}}=-0, \frac{0}{=} \)

Mein Resultat 0 und -1

richtig wäre 0  und 1

Wo liegt der Fehler?

Danke für euere Unterstützung

Problem/Ansatz

Wo liegt der Fehler bei meiner Berechnung

Comments

Du solltest zunächst mit -1 multiplizieren.

Answer 1

-x^2+x= 0

x^2-x =0

p= -1, q= 0

0,5±√(0,5^2-0) = 0,5 ±0,5

x1= 0

x2= 1

Comments

vielen Dank für die schnelle Antwort

Wieso hast du hier ein positiven Wert und kein negativen?

0,5±√(0,52-0) = 0,5 ±0,5

die PQ Formel beginnt mit minus P/2

---

Die pq-Formel geht nur bei positivem x^2.

Ich habe dazu die Gleichung mit (-1) multipliziert.

---

jetzt ist alles klar wieso das nicht funktioniert hatte -> vielen Dank