Aufgabe:
Urne U1 enthält 7 rote und 3 weiße kugeln, urne U2 enthält 4 weiße und 1 rote Kugel.
Mit welcher Wahrscheinlichkeit stammt eine gezogene rote Kugel aus U1?
Problem/Ansatz:
Hallo
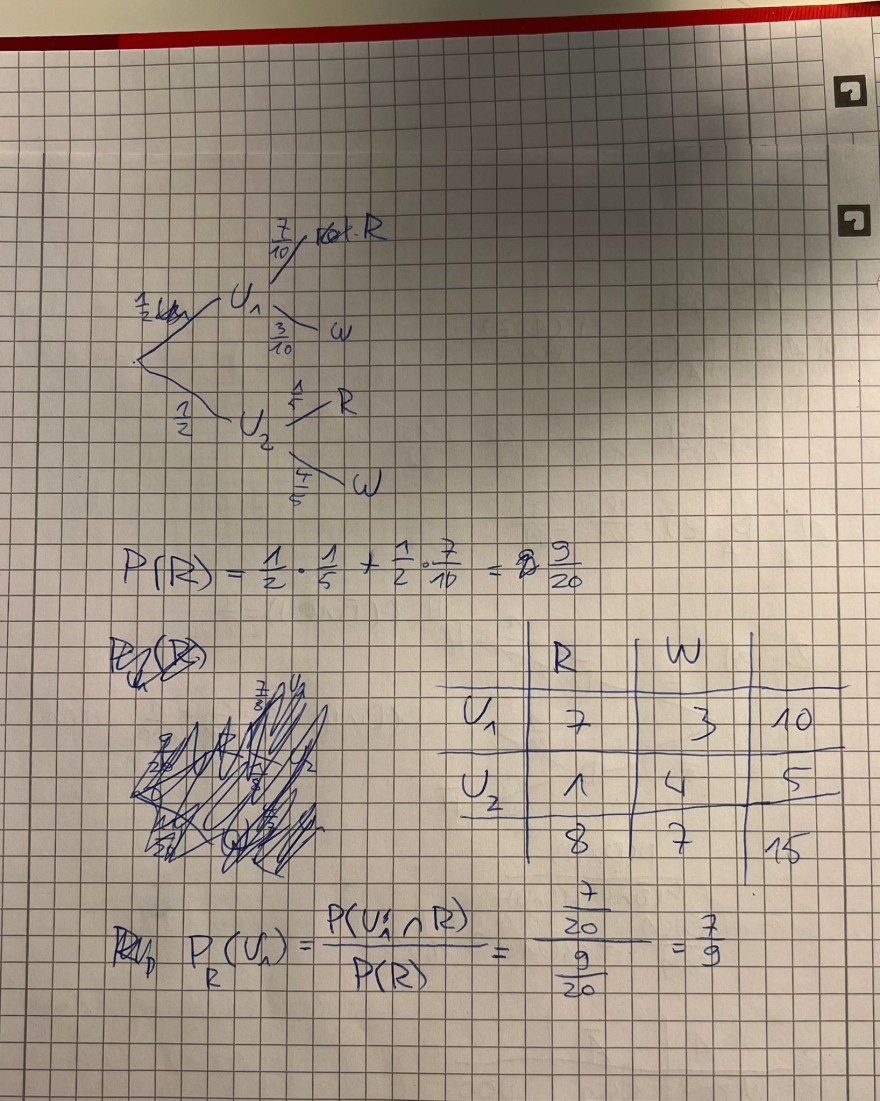
Ich habe ein Baumdiagramm gezeichnet, die Wahrscheinlichkeit P(U1 ∩ R) die ich daraus durch Pfadregeln erhalte ist 7/20.
P(R) berechne ich mithilfe des Satzes der totalen Wahrscheinlichkeit, \( \frac{1}{2} \)*\( \frac{1}{5} \)+\( \frac{1}{2} \)*\( \frac{7}{10} \)=\( \frac{9}{20} \)
Wenn ich diese aber mithilfe der untenstehenden Vierfeldertafel bestimme, komme ich auf 8/15.
Habe dafür P(R) berechnet, wobei ich auf 9/20 kam, aus meiner Vierfeldertafel lese ich jedoch 8/15 ab.
Wodurch kommt dieser Unterschied zustande, wo liegt mein Fehler?