Nachdem die Fragestellerin die Aufgabe nun konkretisiert hat:
Es geht um diese Fläche:
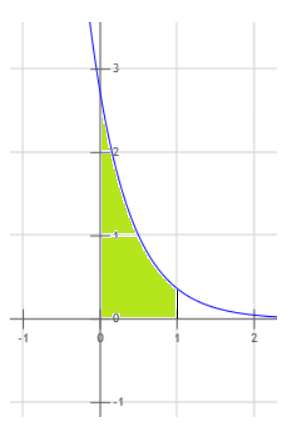
Man integriert die Funktion f(x) = e-2x+1 im Intervall von 0 bis 1.
Um das unbestimmte Integral zu finden, verwende ich Integration durch Substitution. Wie das geht, sollte in Deinem Lehrmittel stehen.
\( \displaystyle\int e^{-2x+1}\, dx = -\frac{1}{2} e^{-2x+1}\)
Und dann mit dem Hauptsatz der Analysis:
\( \displaystyle\int\limits_{0}^{1} e^{-2x+1}\, dx = -\frac{1}{2} e^{-2\cdot 1+1} - (-\frac{1}{2} e^{-2\cdot 0+1}) = -\frac{1}{2} e^{-1} + \frac{1}{2}e = \frac{e^2-1}{2e}\)