Kreisgleichung aus Tangente und Mittelpunkt finden

Question

Aufgabe:

die gerade g:x-3y=17 ist Tangente an den Kreis k mit dem Mittelpunkt M=(3/2).

Man sollte eine kreisgleichung angeben.

Problem/Ansatz:

Wie berechne ich hierr den radius??

Answer 1

Die Distanz vom Mittelpunkt zur Tangente ist der Radius.

Comments

Wie rechne ich das jetzt

---

Zum Beispiel: Eine Gerade h durch den Mittelpunkt mit Steigung senkrecht zu g und dann den Schnittpunkt von g und h ausrechnen und dessen Distanz zum Mittelpunkt, das ist der Radius.

So kann man es wahrscheinlich nachvollziehen und ausrechnen ohne Formeln auswendig zu können.

Answer 2

Die Gerade f durch den Mittelpunkt des Kreises, senkrecht zur Tangente g wäre

f: [3, 2] + r * [1, -3] = [r + 3, 2 - 3·r]

Schnittpunkt von f und g über Einsetzungsverfahren

(r + 3) - 3·(2 - 3·r) = 17 --> r = 2

Radius des Kreises wäre jetzt

2·|[1, -3]| = 2·√10

Comments

Hier noch ein Etwas kürzerer Weg ohne das Lotfuspunktverfahren

x - 3·y = 17

Abstandsformel der Geraden

d = |x - 3·y - 17| / |[1, -3]|

Hier nur den Mittelpunkt des Kreises einsetzen.

d = |(3) - 3·(2) - 17| / |[1, -3]| = 2·√10

Answer 3

$x-3y=17→3y=x-17→y=\frac{1}{3}x-\frac{17}{3}$   →$mT=\frac{1}{3}$→$mN=-3$

mT ist die Steigung der Tangente und  mN ist die Steigung der Normalen

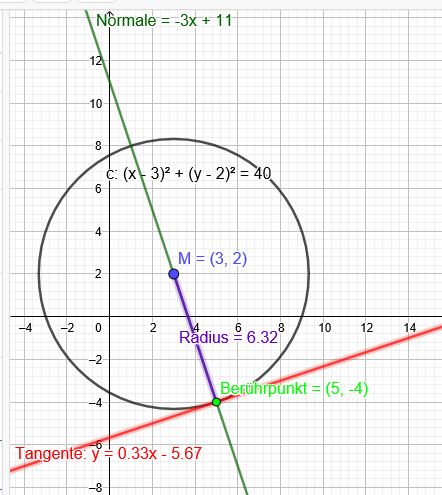
$M=(3|2)$

Normalengleichung:

$\frac{y-2}{x-3}=-3→y=-3x+11$

Schnitt mit der Tangente bringt den Berührpunkt:

$\frac{1}{3}x-\frac{17}{3}=-3x+11→x=5→y=-4$

Bestimmung des Radius:

$(x-3)^2+(y-2)^2=r^2$

Einsetzen des Berührpunktes:

$(5-3)^2+(-4-2)^2=r^2→4+36=r^2→r=\sqrt{40}≈6,32$

$(x-3)^2+(y-2)^2=40$

Comments

Wie kommst du auf die normalgleichung

---

Die Steigung der Tangente beträgt $mT= \frac{1}{3}$ Da die Normale senkrecht auf der Tangente steht, beträgt ihre Steigung $mN=-3$. Für die Berechnung gilt:$mT*mN=-1$

Zur Normalengleichung kommst du nun mit der Punkt-Steigungsform einer Geraden:$\frac{y-y₁}{x-x₁}=mT$